return to homepage
The Solution to Tides
In previous papers I have shown that current tidal theory is a wash, so to speak. In my first paper, I showed that the barycenter is no part of the solution, that the tide differential math was pushed, and that the theory of heaping toward and away from the Moon was illogical. There is no possible cube law, as claimed, which destroys all the current math. This leaves the current data charts hanging. We have lots of good data, but no good way to fit it into a theory. Because we do not understand what is causing the data, our tidal predictions are not as good as they could be. Currently, all we can do is extrapolate data to make a prediction. Since the motions are consistent, this works pretty well. But it would be nice to understand what is causing the tides.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.
return to updates
Part 3
by Miles Mathis
by Edward Poynter
I have come to believe that the standard model of tides knows that what I have just said is true. Since I began working on tides several years ago, I have watched the tidal pages at Wikipedia change twice, both times seemingly in response to my papers. Since tidal theory has not changed in the past three years, one would expect scholarly sources to be fairly solid and unchanging. And yes, Wikipedia is a scholarly source on tides, since the pages are written by the academies and locked. And yet we have seen complete rewrites on the page titled “tide” and on the page titled “tidal theory.” The “tide” page has been completely redone twice. How many times have I critiqued that page? Twice. The “tidal theory” page was taken down for over a year after I made a hash of it, and it has only recently returned, in a new shortened form. The new page is even worse than the old one, since there is even less theory. The way to dodge critique of theory is to offer no theory, and that is what the new page does. The new page jumps right into the equations, then, when those are done, shows a long table of harmonics. No theory is given. For instance, a curious young person might ask, “Why are there two tides every day?” That is the question I will answer here in part 3. But no, no answer at Wiki to basic questions like that. Even the math does not address that question. None of the math since Galileo really addresses that question in any rigorous manner. The math is very complex, but the current theory is very bald, and it hasn't changed in centuries. When pressed to go beyond the math, it tells us that two bulges are caused by the Moon's gravity, one near the Moon and one opposite. The traveling of these two bulges creates the two main tides (called M2). Those are the two semi-diurnal, or twice daily tides, we are told. The other two semi-daily tides, of smaller size, are then given to the Sun, by an equivalent bulge effect. When the Sun tides stack with the Moon tides, we have spring tides, and when the tides interfere, we have neap tide.
Sounds good at a glance, so nobody looks closely at it. But I have shown that it doesn't work. The math is a big fudge. The data shows a 46% variation between “Sun” and “Moon” tides, but the math, done right, shows a 67% variation. Yes, the cube law has to be fudged to match data. They just hope no one will notice. I assume they know they are finessing the math, but it is possible that they are just repeating a fudge of Laplace or Maclaurin or somebody and have never bothered to check it.
Since my first paper on tides, I have caught both Laplace and Lagrange in other equally huge mathematical finesses, so it may be easier now for me to convince my readers that things like this do happen, and happen often, and persist over centuries. The modern science reader simply has too much trust in the big names.
I will show you again that it can't work, even without any math. Let us say that we accept that gravity is the cause of tides. We accept that the main action here is a pulling action from the Moon on the waters of the Earth. It is easy to see how this would create a heaping of waters under the Moon. It is less easy to see how this would create a heaping opposite. We are currently told that the opposite heaping is caused by the fact that the water over there feels less pull from the Moon, since the water is further away from the Moon than other water. But you have to be pretty careless to accept that at face value. Notice that they have just explained the two heaps by two different mechanisms. The near heap is caused by a straight pulling force. The far heap is caused by the differential field. In other words, it is caused by relative inequalities in the field. But just consider that explanation a bit more carefully. Gravity acts like an attractive force, in the same way as magnetism. So let us say the Moon is a big magnet, and the oceans are composed of iron shavings. The near heap is easy to imagine again. But is there any way to get a heap on the far side? With iron shavings, it may be possible, since the shavings that feel the least force move the least. There would be more iron shavings on the near side of the Earth than the far side, creating lower “oceans” on the far side, but there would be a smaller heap on the far side. This would appear to confirm current theory.
The problem is, water doesn't work that way. Water flows, remember? If we now make our iron shavings liquid iron, our far heap vanishes. This is because as liquid at the sides of the Earth is pulled to the near side, far side liquid moves to replace it. With any sort of liquid, what a pulling action would create is a near side heap and lower oceans everywhere else. Water cannot maintain a farside heap, since it would require friction to maintain it. Therefore, this explanation of the two diurnal tides is false. It cannot work in a liquid medium; especially a liquid like water, which flows so well.
Maclaurin won a prize in Paris in 1740 for a paper showing that the Earth would be a prolate spheroid under the influence of the Moon, with major axis directed at the Moon. This is where we get the current math and the current illustrations showing bulges. Nothing much has changed in almost 300 years. Unfortunately, Maclaurin's equations were based on models, not on data, and we have since amassed huge amounts of data disproving his hypothesis and math. Bodies don't in fact deform that way, as we can see from our own Moon. The Moon, in tidal lock around a much larger primary, should deform with its major axis pointed at the Earth. But it doesn't. The forward part of the Moon is not heaped, it is obliterated. It has a negative tide. Nonetheless, we still get Maclaurin's math and illustrations to this day, leading all tidal theory pages. I have called it a farce, but it is actually worse than a farce. It is a crime of science. Continuing to publish math and illustrations that baldly contradict conspicuous data is or should be illegal activity, according to any scientific standards.
Actually, Maclaurin tried to get around my critique above by using Newton's three-body equations that create an ellipse, substituting the water around the Earth for the third body. Unfortunately, that can't work either, since the oceans are not orbiting the Earth. See my paper on Newton's Proposition 66 for more on that.
I can give you another visual explanation, just as convincing. Again, we take the near heap as caused by gravity, a pulling force. But what if the Moon is above land? The Moon cannot heap waters when it is over land. The land masses on the Earth are quite large, and the Moon must physically pass over them in this heaping action. Let us say the Moon is directly above Minnesota. According to the current theory, we should have high tides all around North America, since the water wants to heap at Minnesota but can't get there. Since the distance is about equal, we should see about equal high tides at San Francisco, Boston, and New Orleans. Is that how tides work, in general? No, of course not. The current theory isn't even in the right ballpark. I will show that current theory is once again mainly upside down or inverted. It is lower tides that are caused by the Moon traveling over land, not higher tides.
Yes, the (secondary) answer to the central question, “Why are there two main daily tides,” is “because there are two major land masses the Moon has to cross every day.” And therefore one of the reasons the two tides are not equal is because the Atlantic Ocean is not equal to the Pacific Ocean. As the Moon is crossing Asia, the tide has a chance to recede further than when the Moon is crossing the Americas.
You will say, “Gee, if that is true, it seems like someone would have seen it before you. It is not a very complex or esoteric theory, is it?” No, it isn't, but it requires that a theorist is looking at the problem in a certain way, and up to this time, historically, no one has been looking at the problem in that way. You see, if you start with the assumption that gravity is the main cause of tides, you are immediately lost. As we have seen, the gravity assumption pushes you into differential field equations, and once you start applying those equations like they did historically, you already have the appearance of the explanation of the two tides. So you never bother to even wonder if it might be the two main land masses or two main oceans that are causing some of the variations. It never comes up.
Now, I haven't read everything in history of course. Someone else has probably suggested something like this. But if they did, it is pretty well buried by now. And even if they did, it is very doubtful they were able to make it work. If someone suggested this before me, they likely tried to tie the idea to gravity somehow, since there has never been any other possible mechanism. But the only way to make the idea work is to tie it to the charge field, as I have in previous papers. I have already shown that gravity has nothing to do with tides. I have shown that the main tide is caused by a charge force from the Moon, and that this force is a repulsion, not an attraction. Beyond that, the spring and neap variations are caused by the Sun, but not by the Sun's gravity. They are caused by the Solar Wind conflicting with the charge force from the Moon to varying degrees. Here I will show the more specific mechanisms of tide production, including daily and monthly variations.
We start by reversing the “heap.” There is no heaping. There is a depression, like a large bowl. If the Moon were over the middle of the Pacific Ocean, and you were in a boat right under the Moon, you would be at the center of a very large depression. Yes, this depression has a travel time to other locations, and the current model is not wholly wrong about the “age” of the tide in different locals. But in this case, when you are right under the Moon at sea, there is no lag time. If the Moon is directly above you, you are at the center of the depression. You are lower than the mean sea level (sea levels without a Moon), but the rest of the world is at high tide (or would be, minus time lags). This is because the mechanism of tide creation is relatively simple: when the Moon is over water, it creates a lower sea below it, and this forces all the other water higher. Just take a beach ball into the bathtub, press it down, and see the effect. It is precisely the same.
This mechanism is so much simpler and more logical than the current and historical mechanism. With gravity as the mechanism, we have to imagine a force transferred from Moon to Earth in some magical manner. In Newton's time, this magic was force at a distance. Now physicists pretend they have left that magic behind, but they haven't. They tell us gravity isn't a straight pulling force, it is a differential field. But you still have to have a mechanism to create the field. The field at the Earth is at a distance from the Moon, so how does the Moon transmit the information to the field? Current physicists hide in the math, pretending that math can somehow be the cause of itself, but it can't. That differential math has to be caused by some mechanism, and the mechanism is still lacking. That is why they are looking for gravitons. They tell you this problem isn't a problem, since it is a differential field, but when they are finished throwing dust in your face, they return to looking for gravitons. They do this because they know in their own minds that the Moon must be causing effects by some mechanism. The Moon cannot cause effects by free-floating math or by a list of harmonics.
My charge field solves this problem in one swoop, since we already have a mechanism for electro-magnetism. It is called the motion of particles, either ions, in the case of E/M, or photons, in the case of charge. We already know the Moon and Earth affect each other strongly electromagnetically. We have piles of data confirming it. And once you have defined the field as repulsive, as I have, you have no problems with mechanics. All forces are caused by bombardment: by touch. It is real photons and ions that are pushing the sea down under the Moon. It is not magic or math, it is mechanics. Not only are you, in that boat in the middle of the ocean, in a real depression caused by real particles hitting you on the head, those particles are also making you weigh more.
Gravity also could never have been the cause since the gravitational forces are already balanced by the orbit of the Moon. The tangential velocity of the Moon is already said to balance the gravitational forces between the two bodies, so there is no leftover force to create tides. Forces that are balanced cannot at the same time be residual. They are either balanced, to create a stable orbit, or they are unbalanced, to create real pulls and motions. You cannot have both balance and motions caused by imbalance. The entire theory of tides via gravity has been highly illogical from the beginning.
Think of it this way: the Moon and Earth do not move at each other, right? The Moon stays at a pretty stable distance, and this is due to the balanced orbit. So, the Earth is not moving toward the Moon, as a whole, and it is not moving toward the Moon because the forces are balanced. If this is so, then why would the water move toward the Moon? Water would have to act differently than land, gravitationally, and we have zero evidence of that. In fact, we have huge amounts of well-accepted evidence that all matter responds the same to gravity. Therefore, the current theory is illogical, counter-intuitive, and falsified by all known data. The water cannot move more than the Earth as a whole, therefore the water cannot be heaped by gravity.
I will be told that the Earth as a whole is deformed by gravity, via Maclaurin's equations, and that the reason the water heaps more than the land is simply due to tensile strength. The land resists the pulling better than the water. But again, we have no evidence of that. Physicists still just assume it is true because the old equations tell them it is true. Because this heaping travels so quickly on the Earth, we have no way to measure it relative to the Moon, proving any given number is caused by heaping. But on the Moon, where tidal lock prevents heaps from traveling, we have very strong negative evidence. Gravity simply doesn't work that way. The Moon does not have crustal apsides pointing toward and away from the Earth. Not only is the Moon not oblate to any degree, with apsides pointing anywhere, if anything the Moon shows a negative tidal bulge on the front. That is, the nearside crust is not only not oblate, it is obliterated. The small inner Moons of Jupiter and Saturn also provide very strong and very obvious negative evidence. They are very near the planets and should be deformed strongly. But none are elongated radially like this. Current theory is a fairy tale on most levels. Not only is the theory threadbare (and contradictory) and the math fudged, the theory and math don't even match the most conspicuous data. That is precisely why the “tidal theory” page at Wikipedia is still such a joke. If they had a decent theory, they wouldn't hide it from you; but they don't have one.
Obviously, I can explain the near depression on the Moon, since the Moon is being bombarded by the Earth. But I can also explain things like the small tides in the Gulf of Mexico. Current theory tries to explain this as due to bathymetry, which is a fancy word for sea depth. It also points to the shape of coasts. These things have an effect, it is true, but they have missed the main reason the Gulf of Mexico has smaller tides. The reason is that the Moon has less land to cross over Central America. If low tide corresponds to “Moon over land” and high tide corresponds to “Moon over water,” then when the Moon only has to cross Panama, for instance, there is going to be very little difference between high tide and low tide. The tide won't have much time to go low before it has to go high again, which means the difference between maximum and minimum will be slight. I haven't studied the charts, but I would predict that the less land the Moon travels over, the lower the tides must be in that area. That is the primary reason the tides in the Gulf are small. The secondary reason is that the Gulf, because it is small and has an opening to the east, acts like a lake. The Moon is moving over the Gulf mainly east to west, and since the opening to the Atlantic is on the east, that is the way the tide will travel. The force from the Moon is down, and it acts to flatten everything beneath it over its entire radius. Therefore, when it is over the Gulf, it flattens the tide there. And the only release of energy is to the east. [See below for further clarification on how the Moon affects lakes]. The only tide that can be created in the Gulf is when the Moon is moving west off the coast of Africa, but even then the motion of the tide is mainly north and south, due to the pinching of the major continents. The Atlantic has much more freedom north/south than east/west, and so that is the way the tide tends to move.
This also explains the great variations in the Bay of Fundy. The greatest variations in that bay occur when the Moon takes its longest route over the Pacific and its longest route over Eurasia/Africa. This gives the waters the longest time to rise and the longest time to fall. The third major factor is lag time. The longer the delay, the greater the difference between maximum and minimum. In other words, if the Moon is traveling near the equator, it will cause a quicker response in those waters, lessening the effect of its long travel over Asia. But northern latitudes like Canada will be delayed, since the rise must travel from the equator up to that latitude. A later high tide is the same as a lower low tide, so the difference is maximized. The secondary cause of tidal differences is caused by the route of the Moon over land and sea, not by bathymetry or coastlines.
Therefore, a successful tide predictor would follow the route of the Moon. Since none of the current predicting machines measure the Moon's time over land, the harmonics are all garbage. They work (broadly and in general) only because they extrapolate from current data. It doesn't matter how you title or explain current data, as long as the numbers are good and are charted correctly. You can then push the data in extrapolation by weighting different lines in different ways, until the math matches the outcomes. You then have a “predictor.” But unless you can explain the mechanics beneath your harmonics, you only have a pushed table of data. That is what current charts are.
I have no way of tracking the Moon over land and sea, but I predict that once my corrected mechanics is used, the tables of harmonics can be greatly simplified. For instance, by 1921 there were already 388 tidal harmonics published by Doodson. Now there are many more than that, though most of the newer ones are almost negligible. Only 62 numbers are really significant, and even many of those are not what you and I would call significant. Not only are they not very significant in size, they aren't mechanically assigned. But even some of the largest harmonics are just given names, with only the flimsiest of theoretical assignments. If we just look at diurnal tides, for example, we find eight numbers applied to effects from the Moon, as in “smaller elliptic lunar diurnal” and “larger elliptic lunar diurnal.” If we go to NOAA to find explanations of these titles, we get nothing. We are taken to a page of “definitions”, but these definitions are just the titles themselves. If we dig we find that elliptic numbers are assigned to variations in the speed of the Moon, caused by its elliptical orbit. I find that assignment tenuous, because gravity has nothing to do with the speed of the object, or vice versa. It would be the slightly varying distance between Moon and Earth that would cause any effect, and that variation in distance could not show itself in a 24 hour period. The period of the elliptic lunar diurnals are about 24 hours. Even worse, the period of the larger elliptic lunar semi-diurnal is about 12.6 hours. The distance of the Moon from the Earth cannot change enough in 12 hours to create such a large effect. The larger elliptic lunar semi-diurnal is listed as order 3 by NOAA, which means it is a primary tide producer, the third largest known. Variations caused by an ellipse in 12 hours cannot do that. The Moon's eccentricity is low and it shows itself over a month, not over 12 hours.
I think it is probable that the bulk of these harmonics are misnamed and mis-assigned. In fact, I think they are all mis-assigned. This order 3 harmonic is most likely the Moon crossing the Indian ocean on some vectors and not others. And the higher order harmonics indicate the Moon crossing smaller landmasses like Cuba or the tip of India or Indonesia or the Philippines. Other harmonics would be created by the Moon crossing the Red Sea, the Bay of Bengal, etc. Once we combine all possible landmass vectors with all possible Solar Wind positions, we have a large number of harmonics. But these “harmonics” are all explained by four or five basic mechanisms, not by hundreds.
But before I get to these lesser harmonics, I need to explain the primary harmonic. I have said at least twice above that the landmass vector itself was secondary, so now is the time for me to tell you the primary cause of tidal variation. This will also be the cause of the two daily tides: the two humps on the semi-diurnal charts. These humps are currently explained by the two heaps caused by the force differential from the Moon, but I have shown those heaps are a mathematical mirage. Tides are a charge phenomenon, not a gravitational phenomenon. The gravitational explanation has never been able to explain the variations, but the charge field allows for a pretty simple explanation of most of them. We start with the recognition that the Moon's daily apparent orbit around the Earth, caused by the rotation of the Earth, is inclined just like the Sun's orbit is inclined. That is, the Moon does not travel over the equator. The Sun travels on the ecliptic, and the Moon travels on an inclined path of its own. Now, we are told that the Moon travels west to east. Relative to the sky, it does so, but relative to the ground, it travels east to west, like the Sun. Both apparent motions are caused by the quick spin of the Earth. And it is this quick motion east to west by the Moon that we care about in tidal theory. We want to look at how the Moon physically travels over the landscape: we don't care how it travels relative to the stars.
So the Sun and Moon travel in the same apparent direction. But they don't have the same inclination. The inclination of the Sun is about 23.5 and the inclination of the Moon is about 5 more than that. So the circles they draw on the Earth will not only be in different places, they will be different sizes. Let us say that the Sun is at its maximum in the north, and so is the Moon. They will then draw the circles shown here.
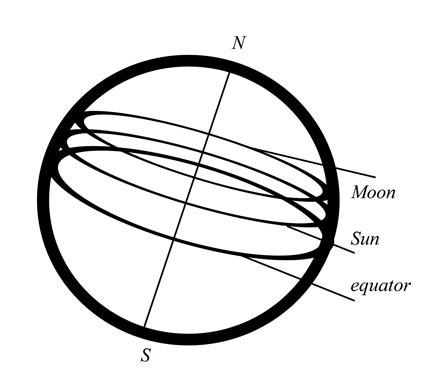
Let us look only at the lunar circle to start with. Here the Moon is furthest from the equator, so we would expect the greatest daily inequality. Why? Because the Earth is a dipole. The inequality is the different distance from north pole and south pole. Remember, the tide is a charge phenomenon, not a gravitational phenomenon, so we can now explain so much more. Think of the charge traveling to the north pole and back: that is one high tide. The charge traveling to the south pole and back is the other high tide. You will ask, “But why are they staggered? The crests are of different heights, which your theory now explains, but on the charts the crests are spaced evenly. Your theory doesn't explain that. In this position, the two tides would be off by only half; and when the Moon was over the equator your tides would be happening simultaneously, wouldn't they?” Good question. It is explained by the fact that the force arriving from the Moon is neither negative nor positive. It is photonic, not ionic, in the first instance. However, once it arrives, it must act by driving free ions. That is how the charge field becomes active in the E/M field. The photons drive ions. Therefore, since the oceans cannot be both positive and negative, the ions can go only one way. The tidal mechanism works in one main direction. And that means that if the tidal force is going south, it cannot also go north. It can get to the north pole only by going the long route—through the Earth. If the Moon is over the equator, it takes about twice as long on one route as on the other. If the Moon is not over the equator, it still takes roughly twice as long on one route as the other, but we get a small inequality. Remember, the input from the Moon is constant, so this is a continuous force we are talking about. We are not just turning it on. We are only explaining the stagger. The stagger is caused by the initial length of route difference, and then the stagger is maintained, like a current through a wire.
We now stack the landmass vector on top of this daily lunar vector, causing another semi-diurnal variation. This gives us the basic shape of M2. This is why M2 is variable itself. M2 has never before been resolvable, but explaining the tide as a charge phenomenon allows us to resolve M2 into its constituents. My proposed resolution is just a suggestion, but I am confident that it is a suggestion in the right direction. Tidal theory must include the Earth as a dipole in order to bypass the historical blockade on progress.
Another charge variation will be explained by the variance of solar and lunar circles, as drawn in my diagram. Let us take just the solar circle, as drawn. Since the Sun is nearer the equator, compared to the Moon, its relative influence will be increased. For two reasons: 1) because the Sun is nearer the equator, the circle is bigger, which means the Sun is influencing a greater area on the Earth, 2) because the Sun is nearer the equator, it will be over the Pacific Ocean for longer than the Moon, increasing its tidal effect. Anytime the Sun is nearer the equator than the Moon, either in the northern hemisphere or the southern, the Sun's tide will be increased relative to the Moon's. On the other hand, when the Moon is nearer the equator than the Sun, the opposite will be true. However, in the southern hemisphere, this rule is slightly different. Part 1 of the rule will be the same. But with part 2 we must monitor the width of the oceans crossed. In general, we get less water as we go north and more water as we go south.
You will say, “Didn't you already explain the 46% variation using the Solar Wind, in part 2? It looks like you are giving us another variation here, by a totally different mechanism.” No, you have to understand that the 46% variation is just an average. That number is the expression of the overall difference between the Solar influence and the Lunar influence. But during any given month, that number fluctuates widely, depending on the positions of the Sun and Moon, and depending where you are measuring the tide on the Earth. Therefore, there are two major variations that requiring explaining. We are required to explain why the Lunar effect is greater as a monthly average, and also why the relationship between Sun and Moon varies so much. Current theory doesn't have nearly enough mechanical complexity. It has a huge amount of “harmonic” or data complexity, but very little mechanical complexity. My unified field allows us to propose many new sources of mechanics, as you see.
Another variation much better explained by my theory than gravitational theory is deep water variations. With tides caused by a pull, these variations are pretty much impossible to explain mechanically. Not only is any pull mechanically impossible, but without a particulate field, it is a joke. With the mechanism as a push—charge bombardment—deep water variations are explained as compression waves. According to current theory, tidal waves are shallow water waves. But we know that isn't true just from looking at the data charts. Many of the nodes on the TOPEX/Poseidon chart are in very deep water. By incorporating E/M theory, and wave production as a push rather than a pull, we simply let the wave travel to the ocean floor and bounce back. It is easy to keep the theory mechanical this way.
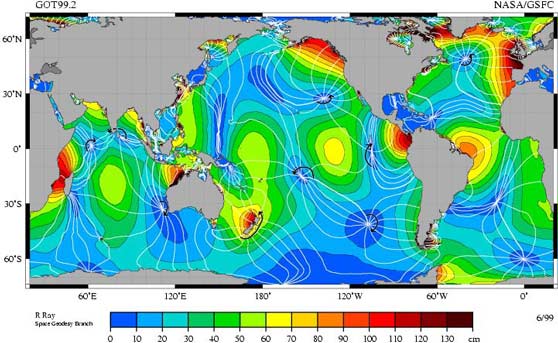
Another major “harmonic” the current theory utterly ignores (at least I didn't see it in the charts) is backwash. Tides generally get larger with increasing distance from the equator, and this is especially true in the north Atlantic, although it is also true in the North Pacific (Alaska, for instance). By my mechanism, this would be caused by backwash. In other words, the tide has to travel up or down from the path of the Moon. But in the north, the tide cannot disperse. It is squeezed by landmasses and ice. It can only go up to the arctic circle and reverse. This basically doubles the high tide in northern latitudes, and the effect is greater in the Atlantic than the Pacific because the Atlantic is squeezed more. The Pacific has much more room to divert this northern tension by releasing it to the south. In the south, the oceans all connect. There is no bottling up of waters. This is why tides are generally low in the southern hemisphere. Only local bottlenecks like New Zealand and Cape Horn create tides there.
In this way, the current table of harmonics is little more than a list of bad titles. It is a compilation of every bad theory of the past, from the bulges of Maclaurin to the shallow water variations of Laplace. The lunar and solar names aren't even used consistently, since we find that in the diurnal charts, for instance, the periods are either around 24 hours or around 27 hours. Obviously, those periods near 24 hours should be assigned to the Sun, and the others are probably lunar. And yet, the main lunar diurnal, which has a period of 23.93, is assigned to the Moon. We also never get any theory about what causes the lunar diurnal. It is listed as separate from the lunar semi-diurnal, so I suppose it must have a separate cause. What bulge causes the lunar diurnal, and how is this bulge created? How can one Moon create so many bulges via gravity?
Finally, in closing part 3, I will show you another failure of current theory, and another explanation of mine. If the Moon creates tides by a heaping effect, then it may be asked why, when the Moon crosses a large lake like Lake Victoria in Africa, it does not vacuum the lake up into the sky, or at least heap it noticeably. If the Moon is powerful enough to raise the levels of all the oceans, it should be powerful enough to effect one lake. And yet Lake Victoria is famous for its lack of tides and currents. Very damning evidence against current theory. But the tables will be turned on me, and the same question will be asked of my theory. The Moon, when passing over the lake, should blast it out of its boundaries, sending the coastal waters many meters higher. Why don't we see this? Once again, the answer is simple: the depression caused by the Moon is much larger than any lake. Lake Victoria is the perfect example to look at, not only because it is near the equator, and must be passed over by the Moon, but because it is the largest lake in the world by area (if you take Huron and Michigan as separate lakes). Therefore, if Lake Victoria is unaffected by a direct pass of the Moon, then no lake can be affected. Think of it this way: remember my analogy to a beachball being pressed into a bathtub's water? Well, what happens if your beachball is larger than your bathtub? The water can't move. The water, and all the land around, will be given extra pressure, but no motion will result. This is why Lake Victoria is unaffected by a pass of the Moon. It is precisely because the lake is near the equator that it shows no tides. Even when the Moon misses it, the Moon is passing near enough that the lake is still entirely within the Moon's depression.
And this is why the Great Lakes do experience small tides. The Moon never goes that far north, so the Moon never passes over the Great Lakes directly. When they experience small tides, they are in caught in the edge of the large depression of the Moon. So we would expect the first tides to be moving north, followed by tides moving south, to bring the water back. This is in fact what is seen. The tides in the Great Lakes move north and south. This is how they are separated from other currents. For instance, the currents in Lake Erie would be expected to flow west/east, since that is the main motion of the waters to the St. Lawrence. If the tides also moved west/east, they would be undetectable, but many have detected small tides in Lake Erie. We are told that Erie and Superior have the greatest tides*, but that should be restated: Superior and Erie have the mostly easily detected tides, since they run east/west. The currents in Michigan and Huron run north/south, so they can't be separated from lunar tides. And we may assume that Lake Ontario can dissipate any tide directly into the St. Lawrence.
I showed the size of the Moon's arriving force visually in part 1, with the illustration showing the emission of the Moon expanding as it moved from Moon to Earth. We simply increase the surface area in a straightforward manner, with distance. The circle of emission from the Moon is 60 times larger than the Earth itself at impact, so the depression is quite large. I estimated that the width of the depression was 1/3 the circumference of the Earth, although this number was more a measure of the influence of the charge at any one time than a true measure of the depression itself. Since the strength of the force is relatively small over any small area, the depth of penetration is small, even at the center, so that the depression doesn't act like a rigid bowl. If it did, the center of the bowl would penetrate the mantle. In other words, our beachball deforms as it presses into the bath water. In the case of the force from the Moon, it goes from being convex to being concave, spreading out across the surface of the sphere.
At any rate, this is all just to show that the force from the Moon arrives over a very large area, too large to create a tide in Lake Victoria. I would suggest that the pressure increase would be measurable, however, and an interesting experiment would be to monitor the water pressure of the lake during a pass of the Moon directly overhead. I suspect that the change would be significant. I would also question the natives, seeking stories of “supernatural” phenomena observed during passes of the Moon directly overhead. Effects on fish and other animals, for instance. These stories might provide a clue of where to look for more evidence.
*http://www.great-lakes.net/teach/chat/answers/100100_tides.html