the solution to tides by Miles Mathis

The Solution to Tides
Part 1

by Miles Mathis

In a previous paper I did an extensive analysis of current tidal theory, proving that the theory fails. I will admit that the theory is ingenious in many ways, since it finds many clever methods for forcing a solution in a field that cannot possibly yield one. For instance, we are told that although the Sun's field is stronger than the Moon's, its differential field changes less quickly, and this differential field is the one that causes tides. Ingenious, but false. The field that causes tides is electromagnetic, not gravitational. Therefore all the math done by the standard model is completely wrong from top to bottom. I show this incontrovertibly in the previous paper, since even with every trick they can throw at the problem, including the barycenter trick, the numbers still don't work out. No tidal theory has ever been successful at deriving the tides we see, and current tidal theory exists only by subterfuge. Once I point out all the fudges, it crumbles into a ugly pile of very dishonest math.

It was interesting for me to return to Wikipedia (which took the brunt of my critique) a year later. The entire page had been rewritten, and all the math deleted. There had been a link to a long page called "Tidal Theory", but that is gone. If you will remember, I said that only Wikipedia was foolish enough to leave its dirty laundry out in the open where people could see it. Every other site on the web, including NASA, was, and still is, publishing broad theories and fuzzy mechanisms. Only Wiki let us in on the math. Now Wikipedia has hired a rewrite from a pro, and we get lots of pretty artist's renderings and macromedia presentations and (almost) fully edited sentences. Unfortunately the content is still the same. Tidal theory still depends on the barycenter fudge and the Sun-causes-the-spring-tide fudge and all the other fudges. They are just packaged much better now, with no math to confuse the issue.

This interests me because it is clear that someone at Wiki is reading my articles. I had spent a few days on the discussion pages at Wiki when I was writing that first paper, and I left some links for the Mandarins backstage. Clearly someone followed them and was highly embarrassed. Possibly alarms went off on campuses all over the country. Someone was questioning the standard model. Man the walls and clean the crennelations!

In fact, this is precisely why the Tidal Theory page had to be scrapped. The discussion page had my critique all over it, and Wiki has no policy for deleting or locking out discussion. The only way to get rid of me was to delete the whole subject. Which they did. No cost is too high in the flight from truth.

This hiding of the math (and so censoring debate) is becoming more and more common, and I expect that physics books at all levels, beginning with high school, will soon become little more than bound four-color computer models and glossy illustrations of dogma, with no math or mechanics to get in the way.

I came across a similar instance of "hide the math" on the web when I did a recent search for Einstein's famous papers on SR and GR. There is indeed a new website devoted to Einstein and his papers, but none of the real stuff is there. We get his correspondence and his papers after 1925, but the famous papers are not to be found. They are quite difficult to find at Amazon or Alibris or even big libraries. It is much easier to get a copy of the Principia than it is to get a copy of any of Einstein's real papers. There are thousands of books on Einstein, but a websearch that seeks his famous papers on Relativity turns up nothing. I don’t think this is an accident. The standard model is in hiding.

It has taken me many months to put together this new theory, since at first I believed that Newton's and Einstein's equations could be made to work. I believed this because I knew that both field equations already contained the E/M field. That is to say, both Newton's and Einstein's equations describe a compound or resultant field. The problem is, tides are caused completely by the E/M part of this field and not at all by the gravitational part.

Although I have shown that gravity is just an acceleration, and that there is no real force imparted by the field, many phenomena have apparent motions caused by the gravitational field that are very real. That is, they are not caused by a push or a pull, but they are measurable phenomena. They register on our eyes and instruments and therefore are just as physical as anything else. Einstein showed that geometry is just as physical as mechanics, and he was certainly correct. One such phenomenon is precession. Another is the orbit itself, both its shape and its very existence.

But tides are not geometric phenomena. They are not caused, in the first instance, by curvature, expansion, Relativity, the time differential or separation, or by any point-of-view considerations. They have nothing at all to do with gravity. Therefore, to solve the problem of tides, we are required to separate out the E/M field completely from the combined fields of Newton and Einstein. Obviously this is not so easy to do. But knowing it was required was perhaps the biggest part of the solution. I have recently achieved the separation, and I now have a Unified Field Equation that is capable of expressing each field individually. This will allow me to compare the E/M field strengths of the Sun and Moon as measured here on Earth, and finally solve the problem of tides.

Before I do the math on the E/M field, proving that it fits the data, I will remind the reader of a problem I pointed out in my paper The Trouble with Tides. It is known that the Moon shows a negative tide in front, where it should show a positive tide. The crust of the Moon has been partially obliterated by some influence from the Earth, but the standard model has no mechanism to explain this negative tide. My use of the E/M field as a bombarding field explains this all at once. If the Moon is being bombarded with photons from the Earth, as the primary mechanism of tides, we would expect the front of the Moon to be obliterated by them. Since the photons are real and the bombardment is real, the Moon must be damaged just as if the Earth were constantly firing bullets at it. In this first part, I will be showing the math for the Moon's influence on the Earth, but in later parts I will be able to show mechanically how the Earth affects the Moon.

The most astonishing thing I have discovered in my Unified Field is that small objects have stronger E/M fields than larger ones. Given two spherical objects of equal density and make-up, the smaller of the two will have a stronger E/M field, not just relatively, but absolutely. The Moon has a field that is 110 times stronger than the Earth's field. This fact seems counterintuitive at first, but a little consideration shows that is completely logical, given the things we already accept about our universe and the way it works. All we have to do is postulate that the E/M field is a real bombarding field or radiation field made up of much smaller bodies.¹ This field is being emitted by every single atom in the field (and even by the electrons in the atoms). Therefore, any field of atoms of any size will create the same E/M field density, provided that the density of the atoms remains constant. A small area of atoms will create the same field as a large area of atoms. If we look at areas that are cubic, then at the edge of any size cube we will find the same E/M field density, given an equal density of atoms in the cube. It does not matter if our cube is one meter across or one light year across.

But if we look at areas that are spheres, we find something strange. If we postulate that all the radiation is emitted radially, as if from the direction of the center, then smaller spheres will create much denser E/M fields than larger ones. This is due to the ratio of the surface area to the volume, of course. A smaller sphere will have the same ratio of mass to volume as a larger sphere, by the definition of density. But it will have a larger ratio of density to surface area, which proves my point.
This is a bit confusing, so think of it this way: the smaller sphere focuses the charge that is emitted, creating a greater charge density. A larger sphere will emit more total charge, of course, but if we look at the amount of charge emitted from a given radial line, the smaller sphere will actually emit more. This is because there are fewer such radial lines with the smaller sphere, so more density has to go with each line. Or, just reverse this logic: as we move to larger spheres, the same density has to emit through a greater surface area. Since the surface area increases faster than the radius, the charge will dissipate into space more with a larger sphere than with a smaller sphere. This is important when we are looking at tidal influences between celestial spheres like the Earth and Moon, and we will see the importance later with other charge influences, like those that cause axial tilt and Bode's law. When looking at linear influences between planets, the charge density is more important than the total charge.

In another paper, I have shown that, given a density of atoms in a sphere, the E/M field density outside that sphere drops off by 1/R⁴. I was able to prove this by looking only at the known gravitational numbers from the Moon and Earth, and subtracting out the acceleration fields. The radius of the Moon is 1/3.67 that of the Earth and its density is 1/.6057, which gives a field strength of 110 times that of the Earth. If the Moon had the same density as the Earth, its E/M field would be 182 times that of the Earth, as a matter of charge density.

According to this theory, the Sun would appear to have no possible effect on the Earth's tides. Its surface area overwhelms its density in this regard, and then we add the distance, which must also dissipate the field. Unless the Sun's density is very much greater than we think it is (1408), its effect must be negligible. Let's do the math. The Sun's density is about 1/4 that of the Earth. If the Sun were the same size as the Earth, its E/M field would also be 1/4. But its radius is 109x that of the Earth. So it’s E/M field at the surface would be,

(.009545)332,900/(11,990)3.92 = .0676 m/s²

At a distance of 1AU, this field would be
(.0676)(696,000/1.5 x 10⁸)⁴ = 3.13 x 10^-11m/s²

Because the Sun is a giant fusion reactor, we do get electromagnetic effects of other sorts here on Earth. Solar flares, solar wind, etc. These cause very positive E/M responses on Earth, as everyone knows. But the standard E/M field of the Sun is caused only by the density and type of atoms present, and that field appears too weak at the distance of 1AU to cause tides. Unless it is postulated that fusion creates a constant boost in the E/M field, it would appear at first glance impossible to link the Sun to terrestrial tides. The standard model has not made this postulate (obviously, or they would include it to answer the gaps in tidal theory) and I am not in any position to make it here.

Some will say that I have shown that the Sun causes a large precession due to curvature on the Earth (3.36 arc sec), which would imply some great force, but this precession due to curvature or expansion is not a force at all. That is to say, it is not caused by a real radiation field. It is caused by apparent motion due to expansion. This is clear from my simple diagrams, where I show that this bending—whether applied to starlight or to precession—can be attributed to expansion alone. Whether you think it is caused by curvature or expansion, it is an effect of the competing acceleration vectors. It has nothing to do with electromagnetism or any other emitted field.

Others will laugh and say, "By your theory of increase (1/R⁴), a satellite 1km across with a density the same as the Moon will have an acceleration at its surface of 10¹³m/s², all due to electromagnetism. It would act like an inverse black hole. And a proton with a density of the Moon would have an acceleration of 10⁸⁵m/s²." Stated in that way, the point seems devastating. If anybody ever got here before me, this would be another place to give it all up as a bad job. But I don’t quit so easily. This point, like all the other points, can be answered without that much effort.

I have already said in many other papers that the electrical field and gravitational field have to be taken in tandem now. This E/M acceleration we are finding has to be applied to the mass that is producing it, and mass is now a function of acceleration, too. As you have seen, mass and gravity are two names for the same fundamental acceleration, which I have shown is L³/T² in my Unified Field Paper. Therefore, we can’t just compare accelerations directly; we have to look at velocities, too. To take a specific example, I have shown that the Moon has an acceleration due to mass/gravity of 2.67m/s². So assuming v_o = 0, after 1s it will have a velocity of 1.335m/s. That is the velocity and distance in which we now must place the E/M acceleration. But if we look at a marble with a radius of 1cm and the same density as the Moon, it will have an acceleration due to mass/gravity of 1.54 x 10^-8 m/s² and a velocity of 7.68 x 10^-9 m/s. If we apply the E/M acceleration to this velocity, we obviously get a much smaller effect.

You see, with the new theory of a compound field, and mass and gravity as acceleration, all things are not in equilibrium regarding velocity. Before, it was thought that things were in equilibrium regarding a velocity due to expansion, since they weren’t expanding. But now the equilibrium is given only to the relative size. Things still remain the same size relative to eachother, since we must keep a visually consistent universe. But velocities are not equal, as I just showed. Since dv’s are not equal, accelerations cannot be compared directly. The only time that accelerations can be compared directly is when they are taken from objects close in size. The radius difference between the Moon and Earth is only a factor of 3, so the accelerations of Earth and Moon can be compared pretty much directly. But when we compare the computed acceleration of the Moon to a little marble, we can’t do a direct comparison. The Moon is moving so much faster during each dt.

It will be said that this offsets only part of the huge numbers, and that is true. There are other factors. Let us start with the proton problem and see what has to be done. I have an acceleration of 10⁸⁵ to account for. Well, the standard model says that the electrical field is 10⁴⁰ more powerful at the quantum level than gravity, so I only have 10⁴⁵ to account for now. I have shown that the number is a relative number (E/M field relative to gravity field) not an absolute number, so I am halfway there. In calculating the difference in field strengths at the quantum level, the standard model assumes the gravitational field decreases with the square of the distance. I have shown that this is false. The inverse square law applies to the E/M field part of the Unified Field Equation, which means that gravity is some 10²² stronger at the quantum level than they thought. That brings me to within 10²³. I have just shown that the velocity due to mass of a 1 cm marble is 10^-9, so a proton would have a velocity due to mass of 10^-22. That leaves me 10¹ out of 10⁸⁵. Not a bad margin of error for such a quick analysis. And I didn’t even have to discuss the density of the proton, which would of course give me more room to play, since it is unknown. I will firm up these numbers in an upcoming paper, but the quick answer needed to be aired here, to deflect uneducated criticism. Those who would scoff at my numbers need to look at how they fit into my Unified Field. The solution to tides cannot be achieved without freeing the E/M field from its historical bounds, and that cannot be done without understanding how I have redefined the Unified Field.

After all that, perhaps the easiest way to see that the numbers must resolve in much the same way they always did is to recognize that I simply give the 1/R² that we used to give to gravity to the E/M field instead. This makes E/M 1/R⁴ while gravity becomes directly proportional to radius.

Before: gravity is 1/R² and E/M is 1/R²
After: gravity is 1/R and E/M is 1/R⁴

But let us move on. If the Sun is not a cause of tides, then we must rule out Venus and Mars as well. This leaves us with only the Moon. How can the Moon cause all the variations we see?

Since the mechanism was always assumed to be the gravitational field, all the historical (and current) explanations have been spectacularly flawed and simplistic. The basic mechanical explanation, one that is still trumpeted by major websites and institutions, is the heaping of waters nearest and farthest from the Moon (with some delay). This mechanism is so naïve it is pathetic to ponder. Even were the force caused by the Moon's gravity, it seems the shape of the field might have been taken into account by these magnificent theoreticians. A force, of whatever kind, emitted spherically by the Moon, must arrive at the Earth spherically. Assuming the field is traveling at or near the speed of light, we can imagine no delay more than a second or two. So the position of high tides relative to the Moon cannot be pushed very far. They must be looked for in very specific places at very specific times, and since this has never been done, we can call it gloriously negligent.

To show the degree of this negligence, let us return to the internet. Wiki presents us with a new illustration to show the spring tide, which puts the Moon and Sun on opposite sides of the Earth. The same thing happens with the Moon and Sun on the same side, but this illustration is better propaganda, since it appears to show the tides being created by direct pulling action. The problem is, to get the correct tidal mechanism working with the Sun on both sides, you have to treat the field as a differential field. This differential field creates tides both front and back, and it does so with either Sun or Moon. But if gravity really creates such a differential field, it must do so with the barycenter motion as well. Amazingly, the standard model still trumpets the barycenter, even in tidal theory, as you will see from looking at the new Wiki page. This is a problem, since the differential field of the barycenter would create tides that totally swamped the Sun and Moon tides, making this spring and neap tide illustration moot. No matter how you look at it, with either gravity as a direct pulling force or with gravity as a differential field, spring and neap tides cannot be explained. This is why Wiki pulled the full mathematical analysis: the differential explanation does not work. This illustration is a fraud.

Before I continue, I must make one more comment on the standard model. It is amazing to find that tidal theory still rests on Newton, Maclaurin, Euler and Laplace. Wikipedia redressed its earlier problems by falling back on more passing mentions of these famous guys. All were great mathematicians in their day, but their tidal theories were garbage even then. It should be highly embarrassing to have nothing to add to this after hundreds of years. Is no one capable of doing a little independent thought? Must we continue to stupidly parrot Newton and Laplace until the end of time?

Here is possibly the meatiest paragraph on the whole new Wiki tidal page. It is the closest the new author gets to doing any math:

The depth of the oceans is much smaller than their horizontal extent; thus, the response to tidal forcing can be modelled using the Laplace tidal equations which incorporate the following features: (1) the vertical (or radial) velocity is negligible, and there is no vertical shear—this is a sheet flow. (2) The forcing is only horizontal (tangential). (3) the Coriolis effect appears as a fictitious lateral forcing proportional to velocity. (4) the rate of change of the surface height is proportional to the negative divergence of velocity multiplied by the depth. The last means that as the horizontal velocity stretches or compresses the ocean as a sheet, the volume thins or thickens, respectively. The boundary conditions dictate no flow across the coastline, and free slip at the bottom. The Coriolis effect steers waves to the right in the northern hemisphere and to the left in the southern allowing coastally trapped waves. Finally, a dissipation term can be added which is an analog to viscoscity.

Wiki's hired pro still can't spell or use the English language, but so what? More important is that this entire paragraph, though trying to be rigorous, is nothing but niaiserie. It is bushwa, babblement. Laplace's tidal equations are all based on gravity as the mechanism, so they are worthless. But even if Laplace had based them on the E/M field, his postulates would still be illogical. Laplace loved mathematics, but he was very thin on mechanics. His first postulate cannot be true. As I will show, the vertical or radial force must be significant and non-negligible, and so must the velocity created by it. Which also falsifies the second postulate. Concerning the third, the Coriolis effect is a tertiary or lower effect, which does not need to be addressed until the major mechanisms are sorted through. It is a terrestrial stirring of the tide, not a creator of the tide. It is here only to give the author more words to capitalize and more esoteric names and effects to drop. And the fourth postulate is just absurd. Here we have been inundated with false mechanics in order to avoid the real questions. Laplace's equations won't tell us where the high and low tides are, and why, but they claim to tell us that variable tangential velocity at different depths is enough, by itself, to cause the rising and the falling. As if tangential velocity, by being variable, becomes anti-gravitational. The author must bury this in the most impenetrable language ("negative divergence of velocity"), otherwise the casual reader might recognize it for the flapdoodle it really is. Then, to finish up, we are treated to trivial "boundary conditions". As if we need to hear about boundary conditions when a basic mechanism hasn’t even been offered.

Before we look for the position of high tides, let us calculate the force from the Moon. How does the E/M force compare to the gravitational force that was thought to apply? It is stronger or weaker? Let us take some numbers from my previous papers. I found that the acceleration due to the E/M field of the Moon is 1.051 m/s^2*, but this is at the surface of the Moon. This acceleration will dissipate with distance, since the field spreads spherically. In fact, it diminishes at R⁴, so we find, at the surface of the Earth,

a/1.050 = (1,738/378,022)⁴
a = 4.7 x 10^-10m/s²

I said above that the charge from the Sun seemed to be negligible, but now that we see the force from the Moon, we find it is only 15 times the force from the Sun. Therefore we may be able to bring in the charge from the Sun as one of the lesser harmonics later (possibly what is now called the Solar diurnal). But it is still not large enough to explain the 46% Solar input we are trying to explain.

The acceleration from the Moon looks too small to do anything, but we have a vector situation here. The Moon is repulsing the Earth and the Earth is repulsing the Moon, so the total repulsion will be a summation of the two. I have shown that the total acceleration of the combined field is .151m/s², but that isn't the number we need here either. What we need is the Earth’s E/M field acceleration at its surface, .009545m/s².⁽²⁾

By this way of looking at it, the Moon’s field is almost negligible. All it does is give the Earth's field something to bite on. Ironic, I think, that all the effects of foreign bodies turn out to be negligible. First the Sun and now the Moon. The Moon only supplies a force to be resisted—an acceleration that awakens the Earth's own E/M field acceleration.

But why is the "bite" at the level of the Earth's oceans, and not at some level in space halfway between the Earth and Moon? It is simply because the acceleration has to have something to accelerate. The combined E/M field has to have a place to work itself out, and the Earth's oceans are the nearest material field. The fields can’t meet in space, since E/M fields don’t work like that. A field cannot express itself upon another field, since the particles in the field are too tiny. A field must express itself in a material field, an atomic or molecular field. We already know that from QED, but it is good to be reminded of it in this place. Of course, in the ionosphere, we do have an ionic field, and we do see lesser effects from this same cause there. But this isn't the time to get into all that.

Now that we have a new number, we can compare it to the old number. What was the size of the acceleration due to gravity, which was thought to cause tides? Well, the acceleration due to gravity at the surface of the Moon was thought to be 1.62m/s², until I showed that acceleration was a compound number. The acceleration was thought to diminish as R², so the acceleration at the surface of the Earth due to the Moon would have been a maximum of

3.34 x 10^-5 m/s² or .0000334 m/s².
In my previous paper on the problems with tidal theory, I showed that the standard model now finds an acceleration from the Moon of Δa = 1.14 x 10^-6 m/s², using the differential field. They try to add 50% more to that, but I show they cannot logically do so, since the Earth is not orbiting the Moon. Either way, with the differential field or the straight gravitational field, the acceleration is much smaller than I have shown is attainable from the E/M field.

Somewhat shocking, isn't it? We have found 286 times as much force using the E/M field as Newton found using gravity. And we found it all coming from the Earth itself.

What is going to shock you more is that we aren't half finished finding the force. All the numbers above come from the E/M fields that I have segregated out of the compound fields of Newton and Einstein. But this force I have calculated of the Earth's E/M and the Moon’s E/M coming together must still meet the Earth's acceleration due to gravity. For at the same time that the two E/M fields are meeting in the upper levels of the ocean, the Earth is accelerating at 9.81m/s². You can give this acceleration to the field or to the Earth, I am past caring; but I have shown that as a vector, this acceleration must be in opposition to the E/M field. [It is 9.81, not 9.8, since I have proved that the solo gravitational field (without the E/M field) is a fraction more than we thought. We have been measuring a compound field all these centuries. But now I subtract out the E/M field, and we have 9.81.] This means that at the center of our circle, we must add 9.81 to .009545.

Good lord, you say. That would mean that a person would weigh more than double directly under the Moon! So let me put it another way. These vectors are difficult to keep in line, I admit. When I say that we must add 9.81 to .009545, that is the same as saying that we must add .009545 to 9.81. Whereas, normally, we would subtract .009545 from 9.81, to get our old friend 9.8. That is how the two fields work when no other body is causing tides. The gravitational force pulls us down, as an effect, and the E/M field pushes us up, as an effect, so the result is mostly down, to the tune of 9.8. But now I am saying that instead of subtracting, we add. The Moon causes the vector situation to switch. So now, directly under the Moon, we have about 9.82 m/s² as our resultant acceleration. And this makes the tidal acceleration

.009545 x 2 = .0191 m/s²
And that is 572 times the maximum tidal force from gravity.

So, yes, you would weigh about .2% more directly under the Moon.** But don’t be too surprised, since this was an effect of the old tidal theory, too. Except that you would have weighed .00035% less. I am changing the size and direction of the change, but the idea is not all that different.

I will answer one final question before moving on. Why does the Moon's presence appear to switch the direction of the Earth’s E/M field vector? I said that when the two E/M fields met, we added them together, which made some sense. But then I said that we added this result to the Earth’s acceleration. How does this make sense, when I created an entire Unified Field Theory to show that the E/M field vector was in opposition to the gravitational acceleration? You will say, "If the vector is in opposition, it must point out. That is why it repulses the Moon. The E/M field is a repulsive field, according to all your novel theories. If so, the Moon cannot reverse the direction of the Earth's E/M vector just by sending in a negligible amount of force (.00000000047m/s²)."

Again, the problem is one of vectors. I have shown that as effects, the vectors of gravity and E/M are in opposition. The gravitational acceleration creates an apparent motion of attraction (the bodies get nearer) and the E/M field creates a real repulsion (the bodies get farther away). But as real motions, the gravitational acceleration and the E/M field are in the same direction. The surface of the Earth is moving outwards. The Earth is also emitting radiation, and this radiation is moving outward, bombarding all things. So in this case the vectors are not in opposition.

This means that when you are solving a problem, you have to be aware of which vectors you are talking about. Are you talking about force vectors, as seen by real eyes or instruments; or are you talking about acceleration vectors that describe the actual motion of the quanta? They aren't the same.

The Moon's presence seems to reverse the E/M field vector of the Earth, because when the Moon is present, we stop looking at the E/M field as an emission of the Earth and start looking at it as a product of the Earth/Moon interaction. We stop looking at it as an acceleration and start looking at it as a force. As an acceleration, we subtract it from the gravitational acceleration, since their effects are in opposition. As a tidal force, we add it to the gravitational acceleration, since they are a vector summation.

This can be stated more briefly in this way: when two vectors are drawn in opposition, they can either be added or subtracted. If the vectors are meant to represent a collision of particles, they are added, since forces in collision add. If the vectors are meant to represent velocities or accelerations that do not collide, then they are subtracted.

Now, where do we look for high tides, in the first instance? Let us say that we have just turned on the E/M field, and we want to see where the very first effects are. We let the field travel from the Moon, spherically, and look where it draws a circle on the Earth. There we should find a complete circle of high tides, surrounding a very large low depression. On the far side of the Earth, we would expect no primary effects, only secondary effects, and we will look at those in Part 2. All we can be certain of is that there will be no heaping or depressing over there at first, since nothing is over there to mechanically cause such a thing.

The two spheres of Earth and Moon-field meet at an angle, as in the diagram.

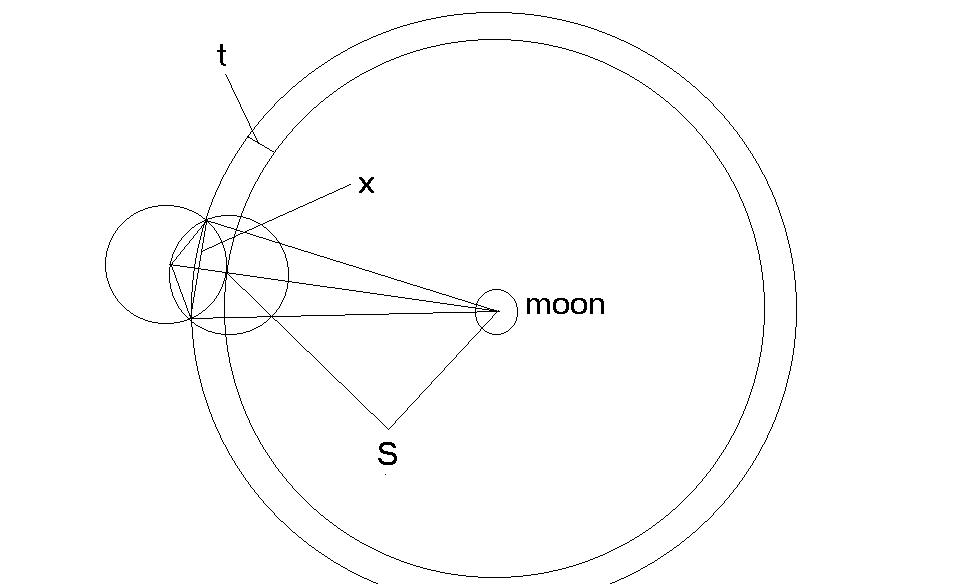
r = 6,378km
R = 384,400km
S = 378,022km
r² = x² + (r/2)²
x = 5524km
sinθ = 5524/6378
θ = 60^o
2θ = 120^o

So the high tides will make a circle with a radius of 6,679km on the curved surface of the Earth. The diameter of influence of the field is initially 13,358km, which is exactly 1/3 of the circumference of the Earth.

Is the number 3 a coincidence? No, it is not. You may assume that any number that precise and that small is not a coincidence, but in this case it is quite easy to show its cause. The cause is the density and radius of the Moon, compared to the Earth. The Earth’s density is 1.65x the Moon’s, and its radius is 3.67x. 3.67 x 1.65 = 6

Not only the strength of the E/M field but its rate of dissipation are determined by density and radius. In the diagram, we are letting the field dissipate with time, in a spherical fashion, as you see. And we are holding the Earth steady. This last is why we find 3 instead of 6. Because we are holding the Earth steady, we are calculating only half of the field changes. We are calculating the Moon’s field moving toward the Earth, but not also the Earth’s field moving toward the Moon. It is an equal and opposite reaction, so it will double the compound field. But we are only calculating the action, not the reaction, so we get half, or 3.

If that was not clear, think of it this way: the orbital distance of the Moon is not a coincidence. I will show this in more detail in another paper; it is not the subject of this one. But the orbital distance, which we are calling R here, is a direct outcome of the two fields, E/M and acceleration (gravity). These two fields cause the orbital distance. The acceleration creates an apparent attraction, and the E/M field keeps the Moon from being caught. The Moon's "innate" velocity is also involved, of course, but the two fields determine this as well, after any amount of time.³ So R is completely determined by the size of the bodies and their densities. The Moon must orbit at (or near) that radius where its field intercepts 1/3 of the Earth's sphere. Study the diagram closely. It is a lovely thing in many ways. It almost looks like a piece of astrology, except that all the coincidences are now explained with simple and clear mathematics and mechanics.

[Some have looked at my diagram and said that the number 1/3 is not even dependent on the Moon; it is dependent on the two small circles I have drawn. But this is not true. If this is not clear at first, consider the variable t that I have marked. That is the differential that brings the Moon into the equation, and it does so since that differential is not arbitrary or accidental. You see, the question is, how far do you let the two spheres of Earth and Moon interpenetrate in the diagram? Which is the same as saying, what is the initial interval of influence? It can’t be instantaneous, so what number do we use? We can’t just draw the larger of the two big circles and do the math with it, since it doesn’t correspond to the first touch at the center. We have to let the first influence wrap around the Earth, you see, and this is impossible to draw. The best way to diagram the interval is therefore the way I have done. This of course begs the question, "What is the value for t?” This brings us to some more math that isn't crucial to the main argument of this paper, so I will put it in an endnote.⁴]

So we have found the size of the acceleration and its initial shape, when it first meets the Earth. What then? From the illustration we can see that the first force will be nearest the Moon, but the other forces in the great circle must come split seconds later. Therefore the initial time lag is not terribly important. What is more important is the direction. In the center of the circle the force is radial. In other words, it comes straight down upon the ocean. We cannot say that this force is unimportant, and that is why I said that Laplace's first postulate was wrong. First of all we have a force that is 572 times any force Laplace could have been working with, most of it generated by the Earth itself. Secondly, this is a force down instead of a force up. A force of that magnitude over that area cannot be negligible.

You can see that the initial force will change from radial to tangential as we go out from the center of our circle. All around the circumference of our circle of initial influence, the force will be completely tangential. But unlike Laplace, I find the tangential force less important than the radial. You will soon see why.

Let's look at depth of penetration. At the actual tangent, the depth of penetration will be almost nothing. The force will be like that of the wind. It will be expected to cause waves, not tides. Only as we move inward from the outermost points of our circle of influence will the depth of penetration become significant, and this depth will be caused by an increasing radial component of the force. This contradicts Laplace once again.

But let's be generous for a moment and try to find an instance where Laplace was correct. If we move inward on the circle a few kilometers, we can cause our force to penetrate to some depth without losing much of its tangential component. We have a nearly tangential force that causes a nearly tangential velocity of the waters. This is the component that Laplace took such interest in, and it is certainly important. I will show that it must be outranked by one other component of the tide, but it is a strong second.

This force is not resisted in any large amount by the ocean, since the water is relatively free to move tangentially. Ahead of this water is only other water until the curve ends, and then there is atmosphere. Both the water and the atmosphere are unconstrained to a large extent. The water has viscosity and pressure and the atmosphere has pressure, but other than that the force is free to act. The mass of the Earth is not behind the water at all to a significant depth, at this angle, so the freedom of the force to act is near perfect (compared to the radial force at the center of the circle of influence). The water can therefore develop a significant tangential speed.

Now, if we look just beyond the tangent—which is to say just beyond our circle of initial influence—we find water that has not been touched by any force at all. It is completely unaccelerated. As our accelerated water meets this unaccelerated water, it will pile up behind it, causing a swell. This is one of our high tides. In the initial stages of our analysis, it must be a complete circle of high tides, with a diameter on the curved surface of the Earth equal to 1/3 the circumference of the Earth. It will travel at some velocity around to the far side of the Earth, until blocked by a land mass or resisted by a reverse tide.

But let us return to our central force. I have shown that it is radial and quite large, 572 times larger than any force we have yet had at our disposal in the history of tidal theory. It hits the Earth like a radial meteor, except that this meteor has a radius of 378,000km. It is like a meteor with a very low density. The main difference between our force from the Moon and a real meteor is that our force keeps arriving continuously. The Earth is hit by this low density meteor every dt, and it keeps getting hit without end. The waters are elastic, and they want to rebound from this force, but because it is continuous, they can do so only to a very limited degree. The freedom of motion is lateral, and so the waters move sideways to the force. Also, this lateral freedom of motion decreases with greater depth. As we go into deeper water, the freedom to move decreases in all directions simultaneously, which pushes the effect up and out on the surface even more quickly. This means that although the force is radial, the motion created is tangential. The water does not want to move down, and at greater depths it does not want to move sideways, either. So the result is motion sideways nearer the surface. Another circular wave is created, traveling out from the center. Initially this central wave is 60^o behind the outer wave, and unless we show that it is moving faster than the outer wave, it will stay 60^o behind it.

But which wave is bigger, the central wave or the outer wave? And what is the ratio? Already it is clear that they cannot be equal, since the mechanism of creation is so different, and this confirms what we know of tides. But to get a usable number we are going to have to do a mountain of math and mechanics yet.

Looking ahead, we see many things. One, we have to include the idea that we have a continuous source of waves from both the center and the outer rim. Two, we have to let the waves travel to the far side of the Earth, where they will interfere. Three, the interference waves have to travel back to the near side, where they will interfere with the source. Four, the Earth’s rotation has to be taken into account, making the continuous sources travel in a westward direction (as a first approximation).

Five, I have to explain spring and neap tides in a logical way, without the Sun's gravitational field (it is worth waiting for, I promise you).

But before we do that in Part 2, we have to look at one other major factor: the magnetic component of the field. Since with the central force we are looking at lateral results, we must remember that the magnetic field also works in this direction. So far all the forces I have postulated and calculated have been electrical forces. But the E/M field has two components. By the right hand rule, if the electrical force is radial down, then the magnetic force will be clockwise, looking down on the ocean. Toward the center of our circle, this should have a magnifying effect on the electrical force, giving it the effect of a screw instead of a nail. This is true whether you imagine once big screw or billions of tiny screws. If the screws were impacting a solid, this would not be true regarding the tiny screws, but since we are dealing with a liquid, we have freedom of motion in all lateral directions, near the surface. The screws therefore cause a spreading, which magnifies the lateral forces already in play with the electrical field. The magnetic field and the electrical field work in tandem to produce the central wave.

At the periphery of our initial circle of influence, we find a different mechanics at work, regarding both fields and their confluence. At the tangent, we have the Earth's force meeting the Moon's, to create a resultant acceleration. But the collision is not head-on. The two electrical forces, by themselves, are orthogonal. This must cause a great reduction in the resultant force, and also cause an angle in the motion of the resultant vector. It will affect the magnetic field as well, since it must suffer the same diminishment. In both cases we will be taking sines or cosines of accelerations instead of the accelerations themselves.

Go to part 2 of the Solution to Tides.

¹The standard model now does make this assumption, finally admitting that the field must be physical and must be mediated by photons.
*See my paper on The Unified Field Theory for a full derivation of this number.
**If this were the only factor, you would weigh .2% more, but it isn't. So don't rush out with your gravimeter: I am not making a prediction here, just doing some math.
³The tangential velocity of an old satellite is caused by the magnetic field working at a right angle to the electrical field. The electrical field causes the orbital radius and the magnetic field causes the orbital velocity. Only very young satellites can be retrograde, and therefore retain a large part of their "innate" velocity.
⁴Once the E/M field reaches the ocean, it can no longer travel at speed c, since it is then conducted by the water. So the time period is determined, in part, by the speed of electricity in saltwater. From the other end, the time period is determined by the gravitational acceleration of the Earth. While the E/M field disturbance from the Moon is racing through the water, the Earth is accelerating outward at 9.81m/s². So, in effect, the tangent of the Earth is changing while the effect is moving from center to tangent. If the Earth was not expanding, the tangent would be near the top of the Earth in the diagram, and we would find nearly half the Earth hit by the sphere arriving from the Moon. That is, x in our equations would be nearly r. Knowing this, we can solve from the other end. We don’t have to ask how long it takes electricity to travel 1/6 the circumference of the Earth, on the surface of oceans; it is easier to calculate how long it takes the Earth to expand from r=5524 to r=6378. Since both times are equal (the period t is determined by when the two motions meet) we choose to do the easier math. At 9.81m/s², it takes the Earth about 13.2s to expand 854km. Therefore, we may assume it takes electricity about that long to travel the given distance. So t=13.2s, the time for one complete "wave" of disturbances to arrive from the Moon. Velocity of E/M field in seawater=506km/s.

If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.