return to homepage
return to updates
by Miles Mathis
milesmathis.com
email:mm@milesmathis.com

In this paper I will explain Relativity in the simplest possible terms. This paper might be called an explanation for laymen, except that it will also be useful to physicists, even those at the top of the field. Relativity has existed in such a partial and muddled state for the last century that everyone might be called laymen with regard to it. There has been no clergy of Relativity, except a false clergy. Einstein, the high priest, understood Relativity in large part, but his explanations only confused the rest of the world. And even Einstein did not understand Relativity in full. That is why he was not able to simplify it. Relativity is much more transparent than we have been led to believe.
I have already published a hatful of papers on Relativity, and one of them has the word “simple” in the title. But even that one was a presentation of the “simple” math. In it I did not try to explain Relativity as a theory, in its simplest form. I will do that now.
As most know, there are two famous forms of Relativity, Special and General. Special Relativity tells us how motion or distance affects our measurements, when we ignore gravity. General Relativity tells us how motion or distance affects our measurements, including the effect of gravity. Gravity is a sort of motion, so it doubles our math. General Relativity is just Special Relativity plus gravity. From now on I will abbreviate SR and GR.
The reason we need Relativity is that physics is a science that relies on light for much of its data. You could say the same about chemistry, in that light has to come through the microscope, but in physics the light is often coming from far away. If you look through a microscope, the light is local light: it is coming from the little lamp under the base. But if you look through a telescope, the light is coming from deep space. It is not local light. Because it is not local light, the images or information that it carries are distorted from the trip. If we receive the image of a star, for example, the image is here, in our eyes, but the star is many light years away. There is a time separation of many light years between the image of the star and the star itself. This time separation distorts the image. To get a non-distorted or normal image, we need to do a transform. This transform is just a simple equation that makes the image normal. Once the image is normal, we can compare it to local images, and know precisely what to make of it.
But it is not only great distance that can distort an image. Great speed can also do it. You already know that great speed can make an image blurry, but Relativity is much more than that. Even if we have a very fast f-stop on our camera, and can get rid of any possible blur, great speed will still cause distortion. It causes distortion because the light we are seeing with must travel from the object to us. But since the object has size, different parts of the image reach us at slightly different times. If we give the object two ends, one end must be further away than the other end. All ends cannot be the same distance, unless the object is a point. And no object is a point, since a point is not an object. This means that we must get distortion, and that the distortion is due to size.
Now, according to this explanation, even an object at rest must be distorted, due to size. And this is also true. But the distortion of an object at rest is so small we may ignore it. To get any noticeable distortion due to Relativity on an object at rest, the object would have to be exceedingly large, so that light traveling from one end would arrive late. Normally, Relativity is not applied to objects at rest, and that is why.
But motion increases this effect greatly, and very fast motion increases it to a point where it becomes measurable. The reason is that very fast motion can make the farthest end of an object seem closer than it is. A small object passing you very fast will seem even smaller, since any part of the object traveling away from you will seem to be compressed. This is called length contraction.
The easiest way to visualize this is to think of SR like the Doppler Effect. In fact, SR is the Doppler Effect on clocks and lightwaves. With mass increase and length contraction, we have more going on than just the Doppler Effect, but the primary effect of SR is an effect on waves.
The Doppler Effect is the stretching or compressing of waves, due to motion. The most common application of the Doppler Effect is to sound waves, and most people have no problem visualizing the stretching or compressing of sound waves. In the standard example, we have the train passing, the sound being higher pitched as the train comes toward us and lower pitched as the train leaves. The sound is higher because the wavelength is shorter, and the wavelength is shorter because the waves have a shorter distance to go each time. At each second, the train gets nearer. We hear the train at 100 feet, then the train at 99 feet, and so on. So the sounds get pushed closer together, and we hear a higher pitch.
Well, the same thing happens with light. Light, like sound, has a wave. The analogy to sound is not perfect or complete, but light does have a wave. A train approaching us will have its light waves compressed and a train departing will have its waves stretched, for the same reason as we saw with the sound waves. We see the train at 100 feet, and then the train at 99 feet, and so on. We don’t see a continuous image, we create one from the still images we receive. Since the later light has less distance to travel, it makes up time on earlier light, and the wave we see gets compressed. In reverse the same thing happens as the train recedes.
Many will think this must make the receding train look longer--since waves that are stretched must be longer--but this is not what happens. The longer waves only make the train look redder. We read longer waves as redder and shorter waves as bluer, so a larger wavelength will cause a redshift.
The reason the receding train looks shorter is that the length of the train is determined by a single image. Unlike the wave, which is built of a series of images, the length is determined by one image only. In other words, we could take a picture with a real camera, and using that one image, we could determine the apparent length of the train. [And, yes, that one image would be distorted by Relativity. That real picture, taken by a real camera, would be distorted by Relativity.] Now, that one image is made up of all the light reaching us at the same instant, from all the points on the train. Since all the light is moving the same speed, the light from more distant points on the train must be earlier light. To say it another way, all the light is reaching US at the same time, to make the image, so it can’t have left all points on the train at the same time. If we work backwards from our eye, and go the speed of light for x seconds, we can reach some points on the train, but not others. This means that our image is made up of older and newer light. For instance, if the light from the nearest parts of the train was emitted at t = .0002s, then the light from the farthest parts of the train might have been emitted at t = .0001s. The light has farther to go, so to reach us at the same time, it had to be emitted earlier. If it was emitted earlier, then it was emitted when the object was not quite as far away. Therefore, the far end of the object will appear closer than it is. Therefore, the object will appear smaller or shorter than it really is.
That was a bit difficult, I realize. It is probably the most difficult thing to understand about Relativity, and it has been misunderstood and misinterpreted millions of times. If you can make sense of that paragraph, you can make sense of any of the subtleties of Relativity.
As one more aid to understanding, I will point out that this length contraction is exactly the opposite of the contraction of sound. Remember that with sound, we found a compression with the train approaching. With light, we find a compression in apparent length with the train receding. Once again, this is due to difference in the data. We hear sound over a series of intervals. A sound takes time. The sound is not just one beep, it is a long whistle. We make up this whistle in our heads by collating a series of sounds. Therefore, pitch, as data, can only be discovered over this series. You can’t get pitch from one wave crest. Pitch is defined and heard as the length between crests, and this length can only be discovered over some longer interval of time, a time that gives us multiple crests.
But length is different than pitch. Length can be discovered from one image, as I showed above. This means that we have to look at how it is measured. We have to study the operation: how the data is processed by our minds or machines. Pitch is compressed while length is increased. It may seem confusing or even counter-intuitive at first, but once you look at the pretty simple mechanics, it becomes clear.
Now let us look at time. Relativity can supply us not only with a length transform, but with a time transform. Which is to say that motion or distance also affects time.
This is easiest to see by returning to the Doppler Effect. We have already applied the Doppler Effect to the light wave being emitted, so we just switch our wave. We make our wave a clock. Instead of letting a train pass us by, we let a clock pass us by. Let us imagine a pulse clock on wheels, passing us by just like the train, on train tracks. If we do this, we see that the pulse clock also has a wave. Each pulse is a wave crest, and the time between pulses is the wavelength. We then apply all I have said above to this clock. We apply the Doppler Effect to the clock. The clock coming toward us will have a smaller period, due to compression of the wave; and the same clock receding will have a larger period. In this way, the clock acts exactly like the sound. To hear the pitch of the whistle, we must hear over an extended period of time, not just an instant. Likewise, to see the rate of the clock, we must watch over an extended period, not just an instant. You can’t tell how fast a clock is ticking from one tick, can you?
This means that a clock approaching us will appear to tick faster, and a clock receding will appear to tick slower. If we use the receding clock to measure time, time will appear to slow down. This is called time dilation.
Notice that time and length change in opposite ways. Time changes like pitch, and therefore like sound. But length changes in the reverse way. Once again, this is because length is an instantaneous measurement and time and pitch are measured over a series.
So we have time dilation and length contraction. Not only are they the reverse of each other, they are the inverse. This is just a fancy way of saying that time slows down exactly at the same rate that length decreases. If one doubles in size, the other halves.
Now let us look at the twin paradox. Although time dilation is true, the twin paradox is not. The twin paradox is even more famous than time dilation, since it was included in films like the Planet of the Apes and a thousand other films and TV shows and books since then. But this paradox is simply the outcome of a misunderstanding. Einstein mistakenly believed that all objects were time dilated. In other words, he defined all objects as receding objects. But all objects are not receding objects. As I have shown, approaching objects are time compressed. They are compressed exactly as much as receding objects are dilated. This means that in any roundtrip, the two effects cancel. They cancel regardless of speed. In other words, you could recede at high speed and return at low speed, and still there would be no paradox, since the distance is the same in either case. You cannot make a roundtrip where your distance out is different than your distance in.
Another famous misinterpretation of SR is that the contraction and dilation is real. It is not: it is only apparent. The object itself does not experience different time or length. Relativity is a theory of measurement from a distance, not an existential theory. It is a theory of how things look, not how they are. Receding objects are not actually shorter, they only look shorter.
This means that all local time and length is equal. All clocks tick at the same rate locally and all meter bars are one meter long locally. This statement is definitional and logical, not experimental, but it can be proved by looking at the speed of light. Einstein began all his proofs and derivations with one assumption: the constancy of the speed of light. Well, if light is a constant, then local time and length must be a constant, by definition. The speed of light c is defined as x/t, so if c is constant, then x/t must be as well.
The transforms tell us this, too. The transform is the equation that un-distorts the image we see. But if we work the equation backwards, we can discover the local field of the object. The local field of the object is the same as our local field. If it weren’t, the equation wouldn’t be derivable. You can only develop a transform by assuming that all local fields are equal. If all local fields are not equal, there is no reason to think you can normalize a distorted image. If all local fields are not equal, how do you know that normalizing the image for your own field is the same as normalizing the image for the object? If all local fields are not equal, then “normal” has no meaning. We can never know that our transform is transforming in the right amount, except by assuming that all local fields are equal.
What this all means is that Relativity is not nearly as complicated as we have been told. It is not mysterious, it is not ultimately counter-intuitive, and it is not incomprehensible. Some parts of it take a bit of thinking, as we saw with length, but even that fell to a simple mechanical visualization.
Now let us move on to mass. The strange thing about mass is that it changes at a different rate than length or time. Most people can’t comprehend why, but the reason comes right out of Newton’s definition of mass. As Maxwell showed, we can use Newton’s equations to write mass in terms of length and time:
F = Ma
F= GMm/r2
Ma = GMm/r2
a = Gm/r2
s = at2/2
a = 2s/t2
Gm/r2=2s/t2
m = 2r2s/Gt2
The variable r is a radius (which is a length) and s is a length, so we have three lengths in the numerator and two times in the denominator. For this reason, mass cannot vary like the time or the length. It must vary in a slightly more complex way. We know that mass normally increases with speed (as in an accelerator), and we can see from that last equation that as length increases, so will mass. Conversely, when time dilates, mass must get smaller. Therefore we may assume that in an accelerator, we are measuring objects in approach.
In many ways, this makes sense, but in one way it doesn’t (at first). It makes sense in that objects can only be detected if they are moving toward a detector. And it makes sense because an object that looks bigger would also seem to weigh more. And it makes sense because time dilates or gets larger as an object recedes. As the object recedes, it must have less relative kinetic energy and therefore less mass. But it doesn’t make sense in that quanta in accelerators are said to gain mass and experience time dilation at the same time. My equations show the reverse.
This contradiction is solved by recognizing that although quanta do have longer apparent lifespans, they don’t experience time dilation. Up to now, it was thought that the two statements were equivalent. It was thought that quanta live longer because they experience time dilation. But this is not true. Quanta live longer because they experience time period compression. Each second or tick of their clocks appear shorter to us, therefore they can experience more of them when measured by our clocks. We measure their lifespans using our clocks, not theirs. Once again, this is a bit tricky, and it has been misunderstood by almost everyone. But if you study it, you will see the logic of it.
Look at it this way. Let us say the quantum is coming right at our detector. If the quantum has a clock, its period will be compressed, as we have seen. By compressed, we mean it seems to us to have more ticks, right? If our clock ticks three times in three seconds, the clock we see coming at us will have 4 ticks, say. It has more wave crests, and would have a higher pitch, if it were sound instead of time. So, we see 3 ticks on our own clock and 4 ticks on the incoming clock, hence time compression. With more ticks, will the object live longer or shorter? Most would say the object must live a shorter life, since it “burns out” faster. If the object has a lifespan of x number of ticks, it must burn those ticks faster when it is time compressed.
But that is not the way it works. The ticks we see are not the ticks the object experiences, therefore this argument is false. The ticks we see are apparent ticks, in our data only, and they don’t apply to any real lifespan of the object.
The correct math is done this way: the object is time compressed, or speeded up. This must mean that it seems to have more ticks than it really has. If it has appeared to speed up, then logically it must have a slower rate when it is not moving. That is what “speeded up” means. Therefore, during every 3 ticks of our clock, we will calculate the object to have lived 4 ticks. After 9 ticks, we will think the object has lived for 12 ticks. Using our clocks, the object will have appeared to gain a longer lifespan.
Experts will say no, Einstein's equations don’t work like that. Time dilation is currently thought to imply more ticks, not fewer. And that is true. But that is only because Einstein’s equations are wrong concerning time. His theory is right, but his equations are wrong. You can see that I have found an inverse relationship between time and length. In his theory, Einstein did, too. He stated in clear sentences that Relativity meant time dilation and length contraction. But then his math stated the opposite. His math shows a direct proportionality between length and time, not an inverse proportionality. This is his greatest mathematical error. To gloss it quickly, he uses these two equations as a starting point for his math:
x = ct
x’ = ct’
Those two equations are supposed to represent the motion of light in two different systems. But in those equations, length and time are directly proportional. If c is constant, then as t gets bigger, so must x. If those equations were true, then time would compress as length compressed. But that is not what Einstein intended to prove. He intended to prove that time dilated as length compressed. His transforms are still said to show that. But in their current form, they cannot show that. They have to be misread and misinterpreted and misapplied in order to make any experimental sense.
I have shown you that it is possible to match experiment and be consistent at the same time. But in order to do that we have to admit that time dilation is an increase in the period, not an increase in the ticks. We have to treat the time period like the wavelength, with the ticks as crests. Once we do that, we see that quanta are not experiencing time dilation. They are appearing to live longer due to time compression. And this is logical because to experience time dilation, they would have to be moving away from our detectors. But if they were moving away from our detectors, we could not detect them.
Now we will move on to General Relativity. General Relativity has been more difficult to understand because it adds one mystery to another. Relativity has always been difficult enough by itself, and even my simple explanation has its hard parts. But with GR we add the mystery of gravity. Gravity is still not understood by any part of mainstream physics, not by the standard model, not by string theory, and not by any of the avant garde theorists in other subfields. Gravity was a mystery for Newton and it was still a mystery for Einstein. Newton did not explain gravity, he only supplied an equation for it. Same with Einstein. He did not explain the mechanism, he only updated Newton’s math to include SR. Currently, we have no mechanism for gravity. The proposed mechanism is gravitons, but we have not discovered them and we have not come up with a consistent theory to contain them. For this reason I will ignore gravitons. The theory of gravitons is not really strong enough to even merit a response.
Einstein used curved math to update Newton’s equations, and it is thought that this math was curved to include SR. But this is not true. The curved math was used to express the acceleration of the gravity field, and Newton’s field was already an acceleration. So Newton could have used curved math himself, without SR. What happens when we add gravity to SR is that the field then has two separate accelerations. The field curves twice. Einstein’s field equations are doubly curved, and no one seems to understand that except me (and now you).
Any acceleration is a curve. That is not esoteric knowledge: they teach it to us in high school. Therefore you can express any acceleration field as a curved field, if you like. But you don’t have to. You can also express any acceleration field as a straight or rectilinear field. By the same token, you can express two overlapping acceleration fields as a straight field. It takes a bit of unwinding, but you can do it. I will show you how in a moment.
Einstein told us that he was required to use a curved field to express GR, but that is false. He used a curved field mainly because he was pressured to do so by the top mathematicians of the time. At first he resisted, but then perhaps he saw the PR potential of a pretty math. At any rate, I am going to skip the curved field, for two reasons. One, the math is difficult and no laymen would understand it. Two, it is unnecessary. The curved math and its explanation is ten times as long as the straight math and its explanation. Using the straight math, there is the possibility I can make you understand GR in just a few pages.
The problem that Einstein faced with GR was the problem of importing SR into Newton’s gravity equations. He needed to do that because in any real problem of astronomy, objects are moving in gravity fields. The transforms of SR aren’t enough to make accurate predictions of motion or energy. Physicists working with particle accelerators can mostly ignore GR, but astronomers cannot.
What makes this problem especially difficult, at first sight, is that the field is caused by spherical objects. At the macro level, all the major gravitating objects like stars and planets and moons are spheres. All the acceleration vectors point in toward the centers of these spheres. You can see why Einstein might think he needed a curved field. The surfaces of the spheres are curved, so how can you use a straight field? Einstein said you couldn’t do it, but I have found a way.
What you do is reverse all the acceleration vectors in the universe, simultaneously. Instead of making them point in, you make them point out. Einstein actually provided the mathematical and theoretical justification for this reversal in a concept he called “equivalence.” In a famous thought problem at the beginning of his GR proof, he showed that “acceleration out” was mathematically equivalent in all ways to “gravity in.” He gave us a man in an elevator car drifting in space, and showed that, given a force, we could not tell if it was a push or a pull. The pull was gravity and the push was an acceleration in the reverse direction.
Strangely, Einstein invented this equivalence principle but then left it hanging. He showed it and then didn’t use it. As it stands now, it is only a clever thought problem with no tie in to his math or theory. On the next page, Einstein began explaining curved space, so he did not reverse his vector. He did not replace gravity with acceleration.
But I have done so. And it turns out that this is the easy solution to GR. The vector reversal implies that gravity is not a pull. Rather, it is a real acceleration outward of all material objects. Yes, it implies that all objects are getting bigger very fast. But the fun part is that you don’t have to accept that as real. You can if you like, but if it is upsetting to you, just accept it as a mathematical manipulation, one that you can reverse later. Mathematical manipulations like this are perfectly legal. Einstein’s postulate of equivalence is a mathematical manipulation just like this, and Minkowski’s four-vector field is another. Richard Feynman was a master of mathematical manipulations, although many or most of his manipulations are not as legal or justifiable as this one.
In other words, we reverse the field in order to make our math easier, then we turn it back around after we do the math, bringing us right back to the world we know and trust.
One way to think of this that makes it clearer to some is to recognize that, given the acceleration of gravity, we must express that curve in our math somewhere. But we are given a choice of where to express it. Einstein expressed the curvature in the relation of length to time, which is the more normal way to express it. It is more normal since it matches the axis assignments we are taught in high school, when we first learn about the Cartesian graph. In the normal Cartesian graph, x is length and t is time:
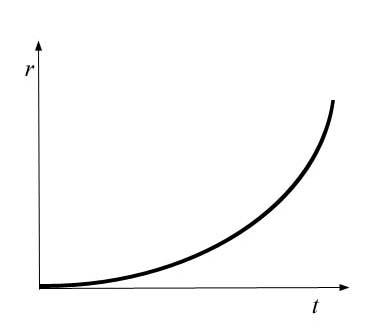
In my new math, I make a different assignment, as you see in the second graph. Instead of assigning the vertical axis to length, we assign it to radius. Rather than assign it to x, which stands for the distance the smaller (falling) object goes in the field, we assign it to r, the radius of the larger object. In this way, the curve is on the size/time graph rather than on the length/time graph. We have expressed the curve and therefore the acceleration, but the curve is no longer on the x/t graph. The x/t graph goes back to being rectilinear, which means we can use old-fashioned Euclidean math. We don’t need fancy non-Euclidean or curved math. We would have to use non-Euclidean math only if we were calculating the relative sizes of our moons and planets, but we can use straight math on the smaller objects in the field.
Once we straighten out the gravity field like this, we can import SR without curving it either. We go from two stacked curves to no curves, which makes the math so much easier. In developing a transform, we don’t need difficult math or concepts, we just need a straight addition of all the effects. Using this straightened field, we can calculate the effect of the gravity field simply by letting the objects expand at their known rates. In this way, gravity is not a force in the math, it is a motion. We let the objects involved expand, and then apply the SR equations to them while they are expanding. It is fantastically easy to do, and it gets the right answer. Using this method, I was able to derive the numbers that Einstein got for starlight bending by the sun and for the perihelion precession of Mercury, as you can see by going here.
Professional physicists may find this useful, especially the engineers, but laymen will unlikely be satisfied by this math. They will say, “That is all fine and good, but what does it mean? What does it tell us about gravity? Is gravity a pull or a push? Is space curved? Are objects expanding?”
My new math is important because it tells us not only that the math does not need to be curved, but that space does not either. The curvature was a choice of Einstein. It was a mathematical choice. This means that space is not curved.
Gravity is also not a pull. Einstein, like Newton, treats gravity as a pull, but their maths, curved or not, are not able to explain all that we see. Newton’s biggest problem was force at a distance. He could not explain how a pull was transmitted through empty space. His theory was flagrantly non-mechanical. Einstein’s biggest problem was impetus to motion in the field. With the curves created by the field, he could explain an orbit or a continuation of a straight fall into a planet, but he could not explain why an object placed in a field would begin moving directly toward the center of that field. That is perhaps the greatest unseen hole in Einstein’s mechanics.
According to the math and the motions, the gravitational field acts like it is created by the expansion of the central objects. Therefore I would say that is the correct default theory at this time. It may be that we can come up with an even better theory, but until we do, I would say that expansion is mathematically and theoretically the most consistent and most satisfying. It is unsatisfying in only two ways. One, it conflicts with our innate belief in and need for stability. Two, it does not include a cause of this expansion. But, as far as number 2 goes, it is no worse than any other theories of gravity. Were you ever bothered to ask what causes the earth to pull? If not, why should you find that to be a strong argument against expansion? Besides, it is always easier to explain a motion than a force. I can’t think of any possible mechanical explanation for the earth pulling, while I can think of several for the earth expanding. As just one example, the earth may be expanding because all objects are still feeling the effects of the Big Bang. All objects are still exploding because the Big Bang happened from the center of all objects, and it is still happening from the center of all objects. We accept universal expansion at the macro-level, why not at the micro-level? If the universe is expanding, why should it expand only at the level of galaxies? Why should it not expand at all levels, from atoms to stars to galactic clusters?
In conclusion, I have shown that Relativity is explainable in simple mechanical terms, most of which are no more difficult to comprehend and visualize than the Doppler Effect. I have shown that all the transforms of Relativity, both SR and GR, can be derived with simple math, with no need for curved fields or difficult operators. We don’t need matrix mechanics, tensors, Hamiltonians, complex numbers, or any of the other mathematical mystifications that we have been assaulted with in the last century. Provided you remember how to do high school level algebra, you can learn to do field equations.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.