return to homepage
return to updates
The Cavendish Experiment
by Miles Mathis

[I won't apologize for the length of this paper: many have enjoyed the story. But if you are only interested in equations, skip to the end. There are plenty of hard numbers and lovely equations there, of a sort to satisfy and shock all but the most jaded. But I don't recommend it. The lead-in is not only necessary, it is a great deal of fun, I am told.]
This is another experiment that has been completely misinterpreted by history. Critics of my papers often lead with the argument that famous experiments like this have been repeated thousands of times by professionals and amateurs alike, some of them very smart people. This argument is supposed to imply a sort of statistical power or infallibility by numbers, I suppose. But it should be clear by now that arguments of that sort are astronomically weak. Any one of us, off the top of his head, could list a hundred instances where centuries of very smart people were completely wrong about a given “fact.” Any study of history will show that most people are wrong about most things most of the time. In fact, all people are wrong about most things all the time. Especially as a matter of science or physics, what we don’t know, as a species, outweighs what we do know by an amount that approaches infinity. So it should be no surprise to find that most of what we claim to know is false, or at best incomplete. It should also not surprise us that the smartest people are wrong almost as often as the dullest. Being what we are and where we are, historically, it just so happens that even our brightest people are not that bright. Due to its rarity, every good idea comes as a shock to everyone, even the one who thinks it.
I daresay it would surprise no one if an alien landed and told us that Newton and Einstein and Cavendish and Feynman were wrong about most everything. We would expect it, really. When it gets right down to it, we know in our heart of hearts that civilization here on earth is in its infancy. We must be aware that technology is only a few centuries old, at most (at least in its current incarnation), and that the majority of our hypotheses are but skeletons. In private moments we are forced to admit to ourselves that gravity, among many other things, is still a great mystery. Cavendish’s experiment concerns gravity, so why should we be so attached to it? We see scientists in other centuries overthrowing ridiculous dogma and we cheer them, but we do not welcome the overthrow of our own dogma. We can accept the new ideas of dead scientists, since the newness is long gone, but we cannot accept new ideas that are new now. Why?
The answers to that are clear, and I don’t think I need list them. I wish I could claim to be an alien or a dead man--in order to get some respect--or to be channeling one or the other, but I can’t. I am nothing but someone who has ideas and the temerity to post them.
The Cavendish experiment is routinely included in a short list of the greatest or most elegant experiments ever done. Like all of the other existing dogma, it has surrounded itself with a nearly impenetrable slag heap of boasting and idolatry, most if not all of it sloppy and unanalyzed. This was true even before the internet arose, but now it is true to the nth degree. Like everything else, the Cavendish experiment has added to its armor a thousand Wikipedia-like entries and glosses by a thousand mid-level physics professors. Of the many thousand recent reruns of the experiment, not one appears to have begun with any level of skepticism. Not one is actually set up to test or extend the experiment. Not one starts with the assumption that Cavendish might have been wrong. Despite the stated sacred nature of the “scientific method”, actually having an open mind about any standard model theory now appears to be equivalent to heresy or sacrilege.
You cannot find anything against Cavendish on the internet. I discovered the existence of one critique by S.J. Barnett, from 1902, but the abstract had recently been deleted by Harvard. Apparently too many people were beginning to look at it, and they had to take it down.
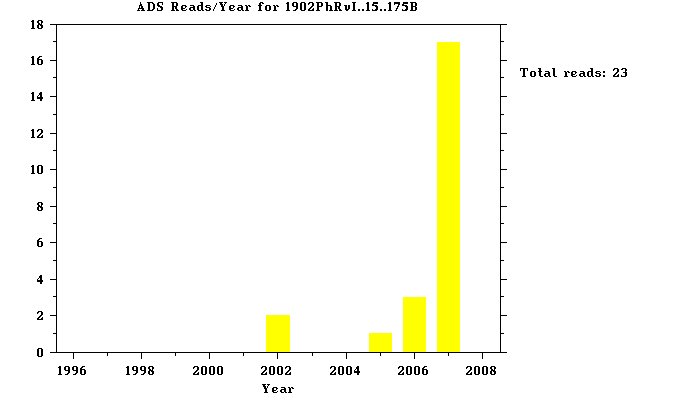
The same was true of other papers listed in adsabs.Harvard.edu. Just to name a few, a paper by P.V. Moore et. al. from IOP, 1994, no longer available as of 2008. A paper by J.K. Hoskins from ADS, 1981, no longer available as of 2008. A paper by Jean Sivardiere from AIP, 1997, no longer available as of 2008. Sivardiere’s paper is titled “Spontaneous Symmetry Breaking in a Cavendish Experiment”, which is highly suspicious. As I have said in another paper, the breaking of a so-called spontaneous symmetry is now code for an experiment that doesn’t work. It is code for a set of “violations”, as in Lorentz violations. Sivardiere is probably telling us about violations in a Cavendish experiment, in other words, showing us where a Cavendish experiment failed. But even the abstract of his paper is now considered dangerous, and it must be taken off the internet.
The only abstract I could find was this one, by P.V. Czipott in STI, from 1983:
A superconducting gravimeter was used in a laboratory physics problem for the first time in the inverse square law of gravitation. The gravimeter test mass was used to measure the force exerted by a 325 kg source mass as a function of the separation between the masses. The results of the experiment are interpreted in terms of two models of non-Newtonian gravity, and compared to limits established by previous experiments. A statistically significant deviation at the level of 7.5 parts in 10 to the 3rd power from Newtonian behavior is observed. It does not conform to either of the non-Newtonian models….
That sounds kind of dangerous to me, and I predict this abstract will soon be deleted as well.
Of course if you work at one of the big universities, you can look up these papers in the library. But those skeptical of the standard model aren’t found working at the universities. Those working at the universities are working there because they have accepted the need for a standard model. Or you can spend $20 to $80 a pop buying them from PRL or APS or IOP online. Or you can look for old books at Alibris or somewhere. But it won’t be easy. My point being that the information is not open, the argument is not open, and finding any counter-argument, even if it exists, is nearly impossible. You can easily find a million variations of the standard model gloss (or, it would be more accurate to say that you are assaulted with them, since they dominate all searches) but all the critiques have been hidden or deleted or priced out of reach. Most of the old books are out of print. You couldn’t buy one if you wanted to. As an independent researcher, you have to travel to a major university and make heavy use of the copier.
You will say that this has always been one of the difficulties of the amateur, or the independent researcher. And while that is true to a degree, it is to miss my point. The scientific method would require that the question remain open, that the information remain open, and that argument remain open, at all times. And yet that is not what we see. The internet has not become a tool for open information, since most of the information in physics is owned by universities or private publishing houses, and they are not open. They claim to share information, but it always turns out that they share only the information they want you to have. That is not an increase in openness, that is an increase in propaganda. The universities are more than willing to share standard model information with Wikipedia and a thousand other sources, but they are not willing to share historical critiques of the standard model. Any time you seek theories or papers or books that run counter to the standard model, you run up against a huge wall. The problem is not only finding the information, it is ignoring all the negative and false commentary surrounding it, meant to drive you away, and the constant chorus of abuse you will inherit with any question you may have. This is true even when, or especially when, these theories come from respected scholars inside academia. For instance, S.J. Barnett was a professor at UCLA, then went to work at Cal Tech and JPL. He was not some crank or marginal character. And he was not an ancient or outdated character: he was still writing for PRL as late as 1953. He specialized in the field of electromagnetism, and wrote a famous book on electrostatics. He said, “Due to the nature of the laws of electrostatics, the experiment of Cavendish is not conclusive.” Dangerous, and now deleted.
None of this is to say that I consider Mr. Barnett or any of the others I have mentioned to be the final authority on Cavendish. I am not here to present their theories, but my own, which resemble theirs not at all. I mention all this only to show once again the sort of world we exist in now, as a matter of science or nescience. The world sold by the standard model, whether it is a world of facts or a world of procedure and opportunity and openness, is not the real world. What we are told is true, and what is true, are two entirely different things.
Before I jump into the analysis, it is best to remind the reader of a few other things, and I will work them in right here. First of all, there was no unit of force until 1873. The Newton didn’t exist in Newton’s time, and it also didn’t exist in Maxwell’s early years. 1873 is only 135 years ago, by the way. Not a lot of time to develop “perfect knowledge” or a bulletproof standard model. Also, Newton’s equation didn’t exist in Newton’s time. Most people don’t know that or have forgotten it. Newton was only working with proportionalities. He also didn’t have G. He had a ballpark figure in his head, using it to propose that two spheres a foot across and having the density of the earth, separated by Ľ”, “would not move to touch in a month's time.” Remember that for later. But G was not his invention. The first scholarly paper with G in the title did not arrive until 1884. We have been making corrections to G up until the present time. As late as 2000 a major correction was made, published in APS with great fanfare. My partial list of deleted papers at Harvard, above, shows the same incomplete state of our knowledge. Papers published in mainstream journals in the past 20 or 30 years differ on the strength of gravity, sometimes by 1% or more. No one has been able to explain the discrepancies, despite the use of what are admitted by all to be very accurate and reliable machines. All this is important here, first because it shows that the standard model is very far from being rock-solid regarding gravity, even in terms of experimental or heuristic science. But it is also important here, since I will show the rather simple cause of these discrepancies.
Now, to look at the Cavendish experiment itself. Let us first analyze the original apparatus. This photo is of a reproduction, not exact in its details.

Cavendish’s actual apparatus consisted of two 12” lead balls weighing 348lbs each. These were the attracting spheres. The spheres to be attracted were 2” in diameter and weighed 1.61lb each. The distance between small sphere and large was 9”. The distance between the two small spheres was 6 feet, and the connecting rod was wooden. The rod was hung from a wire with a torsion angle and restoring action (time) that had already been measured. The two large balls were also suspended, but in Cavendish's experiment they may be considered stationary, since the method of hanging prevented motion. In modern machines, the larger balls are completely stationary, and Cavendish made no attempt to record any motion of his large masses. The apparatus you see in the photo (the line coming out of the wall, on high) was used only to move the large masses into and out of place. The tension on this larger torsion balance was too great to be overcome by the forces involved in the experiment, and so no motion could be expressed in that way. Cavendish measured the deflection of one small ball, and found it to be .16 in.
This is considered to be the crucial information, but I will show that the most crucial has been ignored. We are told that the apparatus was housed in a box to keep out any wind currents. This box was wooden with walls two feet thick. The ceiling was ten feet and the box was 10 feet square. We are told the box was inside a shed, although we are not told what the shed was made of. In illustrations, the shed is shown to be brick, laid parallel not lengthwise, but I could not find any solid confirmation of that.
Now, before I show the solution to Cavendish, I want to show some of the modern apparati that have “confirmed” him. I start with the best and work down. This first one is the largest, but you can see that the attracting spheres are much smaller than those of Cavendish.

I would estimate these large lead balls to be 3 inches, at the most. Pasco tells us they are 3.3lbs, about twice the weight of Cavendish's small balls. In the next one we see even smaller balls.

Here the measurement is done with a laser, and the small balls are encased in glass and metal, to prevent wind. But the large balls are very small, not more than 3” in diameter. In the next one we find an apple as our large mass.

And if you think that is absurd, look at this one.

The small mass is a lead fishing weight, weighing only an ounce or so. The large weights are not pictured, but they are steel spheres about three inches in diameter. This last guy, John Walker of Fourmilab (not to be confused with Fermilab), tells us to make sure to put the apparatus away from the walls, which he has found may skew the findings. This is the only good advice in an otherwise terrible experiment. Despite this it is reproduced all over the internet, sold as a thing of beauty.
We are not told how any of these modern experiments are housed, except by John Walker. He tells us he is in the basement, and that this is a good place to be since it minimizes wind currents. All the other famous experiments that confirmed Cavendish, including Reich (1838), Baily (1843), Cornu & Baille (1878), and C. V. Boys (1895), were done in closed rooms of various sorts, to control wind and other factors. And even this most recent addition to the list of apparati, the small one enclosed in metal and glass, has never been taken out in an open field or on top of a mountain, as far as we know. Every experiment, to date, has been done in a room, with, at most, an effort to be equidistant from all walls, as in Walker’s experiment. I will soon show why this is important.
In the early years of confirmation, there were some attempts to mask the effect, as by placing various blocking materials between the gravitating balls. But since the lead balls were not magnetic to start with, few thought they were masking an electromagnetic effect. Even fewer, we may assume, thought they were masking a gravitational effect, since almost no one ever theorized that a gravitational field could be blocked. In the majority of cases, the experimenters were simply exhausting all possibilities. In any event, no blocking was possible. This seemed to confirm the gravitational theory once again.
There are two main ideas that are new in this paper, as far as I know, and the first one arrives now. These newer machines with very small weights (such as the apple) led me to actually crunch some numbers. An apple weighs, what, 2 or 3 ounces? The other weight in that photo can’t be more than that. We have a bar instead of a ball, but the bar is only an inch or so thick, and can’t have a mass near the end of more than a few ounces. In his experiment, Cavendish found a force at each end of only 7 x 10-8N, and that was with a total mass of 350 lbs. We have a total mass here of half a pound. That is 1400 times less force. And yet we still get a measurable motion.
Is that possible? Look again at John Walker’s machine. That tunafish can underneath is used as a brake. It is filled with water. There is a metal fin stuck into the underside of the Styrofoam bar, and it dips down into the water. This is to keep the smaller weights from moving too fast. But remember that John already has a brake of that sort, although he doesn’t appear to remember it. It is called atmospheric pressure, and it is about 65 N/in2. This pressure acts not only from above, but from all sides as well. In this way, it acts as a brake, just like the water, though with a much smaller effect.
Some will say, no, the air pressure is balanced all around, which creates a zero sum, allowing motion with the tiniest force. But this is false. Air has a viscosity, a resistance, and it cannot balance like that, any more than the water can balance a force in that way. A force of motion in any medium must overcome the resistance of that medium, and air does not have a zero resistance any more than water does. To initialize motion, the force in any direction must be greater than the constant force of resistance. If the force is too small, the object simply will not move. Mathematically, this is just to say that the “drag equation” does not go to zero at a velocity of zero. To initialize motion always require a sufficiently large initial force, depending on the medium.
What John Walker finds is that even with a separation of about 9”, same as Cavendish, and with much smaller masses, he is able to get a motion of the small weight all the way over to the large weight, achieving contact. Some will say this is because his hanging wire or string has no twisting tension, or a twisting tension much smaller than Cavendish’s, but his water brake provides that tension. He also has about the same air resistance Cavendish had, we will assume. But he has a much smaller rod length. Cavendish’s was 6 feet, remember. Walker’s is about one foot. This lessens his effect again, since he doesn’t have the leverage Cavendish had. Torque is force times length, remember; so less length, less torque.
The density of air is 1.3 kg/m3 at 0°C and 1 atmosphere. That is about 2 x 10-5kg/in2. Far from negligible. Using the smallest weights in the machines above, we find a gravitational force of only about F = 2.6 x 10-10N. If we assume that is still enough to overcome air density and pressure (and I have not seen any math to prove that it is), we must nevertheless recognize that we are now in a realm where just about any force, no matter how small, could come into play. Are we quite sure we have ruled all of them out? I am not going to do the math regarding air resistance, since my central thesis does not rely on it one way or the other. I will limit myself here to reiterating that just because we are dealing with a suspended system does not mean that any given force will put it into motion. Any force below a certain minimum amount will not be expressed, and will not lead to motion. Especially with the example of the apple, I suspect that the air pressure between the apple and the torsion bar would prevent the calculated force from expressing itself. If we are to accept these modern variations, I think we require a full mechanical analysis, not just a blithe reference to Cavendish. It is not my responsibility to provide them; it is the responsibility of those who offer us these new machines.
Likewise, if we have now entered the realm of forces of 10-10N, we must be a bit more rigorous with our analyses. Let us first return to Cavendish’s machine. Although he has a force 1000 times greater, he is still lacking the rigor required at his level of precision. We are told that his wooden bar was six feet long, and that his box was ten feet wide. According to my calculations, that puts the smaller balls only two feet from the walls. Those walls were two feet thick. Even though they were made of wood, a wall two feet thick provides a great deal of mass. It may be that those wooden walls of the box were backed up by brick walls of the shed, adding much more mass. How much mass does a wall 2 feet thick, ten feet tall and ten feet wide, provide? Without knowing the wood type and the construction type, it is impossible to say, but we are in the thousands of pounds. A brick wall one foot wide would double that mass, at least, although the brick wall would obviously be two or three feet farther away from our small lead balls. At any rate, we have absolutely huge masses at no great distances from our machine, a machine that is claiming to measure tiny gravitational attractions. I find this monumentally strange.
It is even more strange now that we have apples weighing only ounces standing as proof of gravitational theory, the weight and density of the earth, and the accepted value of an important constant. That is to say, we now accept apples as having easily measurable and verifiable gravitational attractions, but we ignore the gravitational attractions of walls weighing thousands of pounds. I can only imagine that we do this because walls are not made of metal, or walls are not spherical, or something. I can’t really fathom it.
At first glance, it must be clear that the walls of Cavendish’s box and shed cannot be ignored. Even if we look at them only from a gravitational perspective, there is simply no way they can be ignored. The ceiling and floor can be disregarded, perhaps, since the balance is not free to move in those directions. The earth’s gravity constrains all motion in that plane. Call that the z-plane. But in the x/y plane, we have motion constrained only by air resistance and possibly the electromagnetic field. We must not ignore mass in that plane. This means that the four walls must be taken into account, not only as blockers of wind, but as suppliers of mass and any possible E/M interaction.
This is clear, I think, with Cavendish, and it is equally clear with Walker and all modern machines and environs. Walker is in his basement, surrounded by tons of earth. And yet he completely ignores this. He thinks that because he has gone to the center of his room, he has exhausted the boundaries of rigor. Other experiments are done in massive modern buildings that weigh thousands of tons, and that may have any number of different E/M fields, some created by the earth, some created by the iron beams in the buildings, some created by electrical networks in the building. None of this is considered. It is claimed that these considerations are probably negligible, since the forces would be so small. But if we are using one of these tiny modern machines, our forces are already so small they are barely able to override residual air resistance (if in fact they can). We shouldn’t just assume that these things are or are not happening, we should have to prove it. We should have to show that unequal masses are not skewing or wholly creating our outcomes.
More proof of this is found in the experiment of C.V. Boys, the last of the great historical confirmations and extensions of Cavendish. Boys’ paper that he delivered to the Royal Society in 1889 is actually online, complete with illustrations.^ This is not terribly surprising, since it confirms the standard model, despite being a big awful mess. Here is the illustration of his machine.
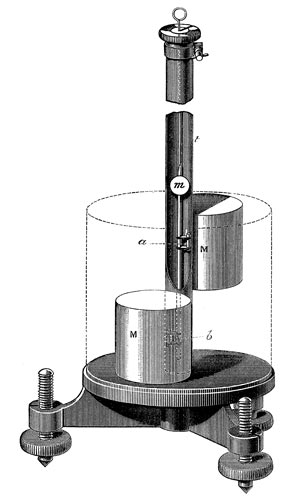
You can see that although it is much smaller, it is of the same type as Cavendish. It has a very heavy stand and large weights that are ludicrously close together. If this experiment had been only about mass, these weights must have conflicted with each other. Boys shows a lot of charts to prove he thought through all this, but they don’t convince me. I am not going to analyze all his charts because my argument here can do without it. Even if he is right in these charts (he is not), it doesn’t matter. No, the problem is that he has entirely too much unanalyzed mass around his machine, and he is saved only by a compensation of errors that I will show later. I mention him because I want to include these quotes from his paper.
First, he says of his precursors Reich, Baily, Cornu and Baille, that in their experiments “the attracting masses have been made as large as possible, and they have been brought almost into contact with the sides of the long box in which the beam is suspended.” This saves me from having to criticize them, since he has done it for me. I have it here from a greater authority than me that the masses were nearly in contact with the box. He also says, “As Cavendish proved…[there were] enormous effects of air currents set up by temperature differences inside the box.” We don’t hear much of that anymore. We are supposed to assume that Cavendish solved his wind problems by building the box.
Next he says this:
With such small beams as I am now using it is much more convenient to replace the long thin box generally employed to protect the beam from disturbance by a vertical tube of circular section, in which the beam with its mirror can revolve freely. This has the further advantage that if the beam is hung centrally, the attraction of the tube produces no effect, and the troublesome and approximate calculations which have been necessary to find the effect of the box are no longer required.
See that he admits that he has not done any “troublesome calculations” on his box, just assuming it produces no effect.
You can see that he has both an inner tube and an outer tube, though the outer one is just suggested in the illustration. He assures us that neither his small weights nor his large ones touch either tube, but they are very very close. Also notice that his lower large weight is very near the heavy mass of the brass base, while the upper one is not. No commentary from him on this, and none from history.
Here’s another one on Cavendish:
In the original experiment of Cavendish there seems to have been an irregularity in the position of rest of one-tenth of the deflection obtained, while the period showed discrepancies of five to fifteen seconds in seven minutes.
Those are two separate margins of error, so they have to multiply. Ten percent times 3 percent. That’s a thirty percent error. We don’t hear much about that from Wikipedia. Boys also admits some shocking things about himself:
I have placed the apparatus in a long narrow vault under the private road between the museum and the Science Schools. This is not a good place for experiments of this kind, for when a cab passes overhead the trembling is so great that loose things visibly move: however, it is the only place at my disposal that is in any degree suitable. A large drain pipe filled with gravel and cement and covered by a slab of stone forms a fairly good table…
During the observations there was an almost continuous tramp of art students above, producing a perceptible tremor, besides which two vehicles passed, and coals were twice shovelled in the coal cellar, which is separated from the vault in which the observations were made by only a four and a half inch brick wall. The result of all this was a nearly perpetual tremor, which produced a rapid oscillation of the scale on the cross-wire….
Boys seems to be begging for funds here; but it is interesting we don’t ever hear these things from the standard model. History has been whitewashed, as you can see, and reading only the modern press reports you would never come away with a real feeling for history or the ways of science. I predict this paper will soon come down as well. Good thing I saved a copy. The important thing to notice here is that Boys is underground, surrounded by huge masses, all of which he ignores. He also ignores his table, his base, and his tubes. And this is supposed to have been the most subtle experiment on G, due to the fact that he used a quartz filament to hang his small weights. OK.
Let us leave Boys and return to the main argument. Basically, Cavendish said that because he showed a motion, and because there was no other known explanation for it, it must be gravity. Newer variations on Cavendish do the same. They show a motion, tell us it is not wind (showing us the metal and glass casing to prove it), tell us there is no other explanation for it, so that it must be gravity. They therefore apply the gravitational equation to it, and spit all the old numbers out as supposed proof of something.
But it is proof of nothing. Cavendish didn’t even bother to include the weight of his walls. He had a 348 lb ball 9” away, and a multi-thousand pound wall 24” away. Sure, only one point on the wall is 24” away; other parts are varying distances, but the wall is not negligible however you look at it. Cavendish assumes an inverse square law but then doesn’t apply it to the greatest masses in the vicinity, even though they are quite near. According to the equation and theory he is trying to use, and that he has been used to prove, he should apply the equation to all the walls, determine force differentials, and go from there. Instead, he just ignores all these things. The fact that he is able to get good results despite ignoring all these things does not imply that his assumptions are all correct, or that it was OK to ignore all these masses. It implies that the motion is not caused in the way he assumes. In an experiment about mass, you should not be able to ignore most mass in the vicinity and still get the same answer. If your set-up doesn’t matter, your set-up is probably wrong.
The same applies to Walker and the new experiments. They are incredibly sloppy about mass in an experiment that concerns mass, and yet they always seem to get reliable results. Does no one else find this the least bit strange? All they have to do is block the wind and the experiment provides all the right motions. They can switch it from clockwise to counterclockwise without concern: they still get attraction. They don’t have to worry if one wall is bigger than the other, or if there are magnetic fields in the area, or if they have cameras or ladders in the way, or if they are not square to the wall, or if they are nearer the floor or the ceiling. All these things that you would think might matter in an experiment concerning mass don’t seem to matter. Very curious.
You should find it very mystifying that all these scientists not only ignore huge masses only two feet away, masses that may or not be balanced, they also ignore the need to say why they can ignore these masses. In other words, they ignore these facts, then ignore their own ignorance of these facts, and none of it seems to matter. We are such blessed creatures, apparently, that we can stumble on the correct answer every time, without even being fully conscious.
Now, I will show you why these things can, in fact, be ignored. But I will do you the favor of giving you a full mechanical explanation of how the forces balance. All the forces, not just the ones we choose to focus on. But in doing this, I will not be able to create an apologia for the standard model or for Cavendish or Walker or anyone else. I will not confirm their assumptions or fill in their blanks. Unfortunately, the correct answer leaves them all completely out in the wind.
To begin, we must go back to one of my first postulates. That is that there can be no attractions. An attraction is a non-mechanical idea. There is no possible trading of particles that can create an attraction. Modern physicists have understood this. That is why they have “no force at a distance” on their T-shirts. Unfortunately, most of them think that gravitons or curved space solve their problem, but neither one does. Gravitons might possibly give us some new sort of repulsion, via bombardment, but no trading of particles can create an attraction, no matter how much new theory you invent along with the particle. Curvature cannot create attraction. Curvature can create curvature, and that is all. Attraction is not curvature. Curvature can explain orbiting, at a stretch, but it cannot explain straight-line attraction. What we see in Cavendish is not curvature, it is straight-line attraction. The smaller ball is not orbiting the larger one; it is moving right at it. Yes, the motion may have a tiny arc, due to the use of a sort of pendulum, but this arc is not part of any orbit or Einsteinian curve. This curve has an end-point that would hit the center of the large ball. Curves in “curved space” don’t do that. Gravitational curves created by bodies never intersect the center. They can’t, logically, because the center creates the curve. Try drawing a curve with a protractor that intersects the point of the protractor. None of the new theories or spaces help us here. These new guys can call their new experiments “bending spacetime in the basement” but that does not make it so. There is no spacetime being bent in any Cavendish experiment. What we have is an attraction, and we must find a way to explain it sensibly.
In other papers, I have dismissed gravity as only “apparent attraction”. That is, I say that gravity is not a force, it is a motion. This motion causes an apparent attraction. But in Cavendish this explanation appears to fail. A reader reminded me of this recently, and he is correct. That is why I am on this page this week solving this problem. I have long recognized it as a real problem, and I now have the theory in hand to solve it. Only my work in the past half year has given me the tools to solve it.
In Cavendish we do not have an attraction that we can explain as only apparent. It is not geometric only. No curvature can explain it, since it exhibits not only motion but real force. The force on the torsion wire is not only apparent. It is a real force. This causes any mechanically inclined person to have fits. It should cause curved space people to have fits, but they aren’t terribly honest with themselves. Only those who have some connection to expansion theories really take this question as seriously as it should be taken. Not only because it is a real thorn to expansion theories, and always has been; but because it is a real thorn to anyone who thinks physics is mechanics and only mechanics. Anyone who demands a real physical explanation of physics must get stuck here, since physics itself is stuck here, and has been since Newton.
There is a two-part answer to this, and the first part is that although gravity is not a force, it is certainly capable of creating a force. In other papers I have shown that logically, gravity is most efficiently explained by expansion, both as a matter of math and of theory. In the first instance, this makes the attraction only apparent and the diminishing distance only geometric. Gravity is a three-dimensional acceleration, and we already knew this from the nature of g. The dimensions of that constant are the dimensions of acceleration, not force. However, we also know that any acceleration can create a force, and gravity is no exception.
A proton expanding into the void is only geometric. But in the real world we have no voids. In the real world a proton or planet expanding gravitationally is not only geometric, since it may be expanding in an atmosphere or, at least, an electromagnetic field. The expansion of the sphere, at whatever level, is certainly capable of exerting pressure on whatever it meets--whether another body or atmosphere or field. If the expanding sphere could not create a force, then the acceleration would be physically meaningless. To have an acceleration without a force, you would have to postulate an infinitely collapsible shell of the sphere. All matter would be inter-penetrable. That is to say, all matter would be a ghost; all matter would no longer be matter. All your “something” would thereby become “nothing.” Acceleration implies that you have a something to accelerate. The verb implies the noun, requires it. Acceleration of an infinitely collapsible shell would not really be acceleration, would it? Logically and definitionally, acceleration must imply force. This connection is not one that Newton invented or defined, or anyone else. It is a logical connection, absolutely necessary, pre-existing any mind.*
That said, it still does not explain Cavendish. If we explain gravity as real expansion, then we must see that we have two spheres, both hung, and both of which want to expand toward the other. If they were unconstrained and in a void, they would do so, and the bigger one would do most of the real moving. That is to say, it would do most of the actual eating up of the space in between, since it has the greater acceleration. But that is not the situation we have. We, the observers, are getting bigger at the same rate as the balls, so we don’t see them expand. Beyond that, we have all sorts of constraints on the motion of the balls. The large ball is constrained by Cavendish himself: the machine includes a stabilizer that prevents the large balls from moving. And the smaller ball is constrained by air resistance, the twisting tension on its wire, and the inertia of its twin (in ascending order, we assume). Since gravity is a motion outward from the center, the smaller ball could certainly express a force against air resistance or air pressure. But it would do that in all directions equally. If it were free to move, it would push the air between it and the large ball away, and move closer, but it is not free to expand into that space. It is constrained by the apparatus from doing so. The apparatus expands just like the spheres and you and me. It therefore constantly creates more space in between the balls, automatically. The big problem is that we must assume the wire is connected to the center of the ball, and the center of the ball is not affected by expansion. Even if we admit that the wire was probably attached to the top middle of the ball, that still doesn’t help us. Expansion cannot work against either the torsion or the moment of inertia, no matter how you express them in your equations. This is all to say that expansion can push, but it can’t pull. It can create real forces, but not pulling forces. A pulling force is equivalent to an attraction, and is logically impossible.
What solves this, in part, is that it is known that Cavendish found it necessary to measure his “attraction distance” while the smaller ball was in motion. The ball never stopped moving. He was able to minimize this motion, but not to stop it completely. This fact is usually mentioned only in passing, with no importance attached to it, other than as a cause of indeterminacy or margin of error. But it has a much greater importance than that. It solves our current muddle completely and unequivocally, since it allows us to make the force a push once more. We wait until the little ball is already in motion toward the big ball, then we let the expansion add force in the direction of motion. In that direction, it pushes more against the air. This allows the acceleration to express itself as a force without ever resorting to a pull or an attraction.
You will say, “That is quite clever, but it only solves half the problem, at best. You have avoided a pull by never requiring the ball to move from a dead stop in the direction of motion. But you have also avoided seeing that the reverse must also be true. If the expansion pushes an extra amount against the air when the little ball is moving toward the big ball, it will also push an extra amount in the reverse direction. It will only tend to increase the angle of swing, but will not cause attraction or the appearance of attraction.”
Quite true, in part, and I happily admit it. I am able to do so since it dovetails with the second part of my answer. First of all, we must assume that the air resistance is less than the other factors, else the ball would never move at all. If the air resistance was as great a constraint upon the small ball as the moment of inertia and wire torsion and so on, we couldn’t possibly have a successful experiment here. Everyone is assuming that the air resistance is negligible compared to the wire torsion and the inertia and the gravity, otherwise Cavendish couldn’t have set these last qualities equal to each other, and found one by knowing the others. Therefore, if the expansion is equal in both directions, adding the same amount of force in both parts of the swing, it is quite obvious that motion will be greater in the direction of least resistance. The least resistance comes from the air, so the small ball moves in that direction!
I think that would be enough to make this paper worth writing, but it is still only half the answer. We still have not addressed the masses of the walls and so on. And we now have to also ask why the little balls will not stop moving. I said I would address all the issues involved here, and I am a very long way from doing that.
I have recently shown that Newton’s gravitational field is in fact a compound field made up of both the gravitational pseudo-field and the E/M field. That is to say, Newton already had a unified field equation, he just didn’t know it. His equation doesn’t include relativity, neither general nor special, but it does include the E/M field.
Up to now, the E/M field has only been understood in the presence of an electrical field, as in a flow of electrons, a current or other type of mass motion of electrons. This electrical field creates an orthogonal magnetic field, and these fields are what most people think of when they think of the E/M field. But the E/M field at the quantum level is not caused by a flow of electrons. The E/M field mediates the forces between protons and electrons themselves, at the most basic level, and this field is not a flow of electrons. That would be a reductio, obviously. No, the E/M field at the most basic level is mediated by some sort of photon, and most quantum physicists now recognize that fact. It may not be a photon exactly like a light photon, but there is some tiny carrier of radiated energy. I have proposed that this level of interaction is an interaction of simple bombardment. All protons and electrons emit a field of photons, and these photons cause repulsion by simple bombardment. This would give all particles a positive “charge", at this level, and would mean that all foundational E/M force is repulsive. Only when we begin to talk of electrical fields caused by flows of electrons can we talk about positive and negative charge, and that charge is caused only by differentials in field strength, or by what is called potentials. I won’t get into how photon fields and electron fields differ, or how repulsions in one create both repulsions and attractions in the other. That is not the purpose of this paper. [Go here for the full explanation.] I only want to point out that I have created a new meaning for the E/M field, as it pertains to quantum particles. In my theory, we now have a foundational E/M field, which is created by all particles and which is always repulsive; and a sort of uber-E/M field, which is the field of electrical currents and flows, and the other effects created by them.
For the most part, none of this is revolutionary. I am not claiming to have discovered most of this. In fact, much of what I just said is accepted by the standard model, and I got it from them. My only addition is to make the basic field uniformly repulsive, and to explain electrical or quantum repulsions in slightly novel ways. I do this, obviously, to once again get around the idea of attraction as a real force. I do not believe in attraction as a real force, since no one has ever explained it mechanically, and since I don’t believe anyone ever shall. I have argued elsewhere that it is logically impossible to do so, and this is true in E/M theory just as it is in gravity.
In recent papers I have shown that this basic E/M field must be created by all objects, not just magnetically charged ones. Lead balls must emit it, and wooden bars, and paper, and everything else. It is emitted as a function of mass, since it is emitted by the elementary particles themselves. Like gravity, it is not a terribly exciting or important force at the level of everyday objects. It only takes on exciting dimensions at the quantum level, where it is not measurable by normal instruments. But, unlike gravity, it does not get exciting at the level of planets or stars either. Its importance is small at the level of a pool ball, and smaller yet at the level of a star. That is why it has always been ignored, except in quantum mechanics.
But at the level of a pool ball, it is not negligible either, especially when we begin studying forces of 10-10N. It is here, at this level of precision, that we can subtract it from Newton’s unified field equation, and get something that is a meaningful fraction of the total field. In my unified field paper I have actually separated the two fields, showing the two separate equations that make up Newton’s famous equation.
As it turns out, from the level of size of a quantum to a grain of sand, the E/M field swamps everything. We already knew this. From the level of size of the earth to the largest galaxies, gravity swamps everything. We already knew this, too. What we did not know until now is that from the level of size of a grain of sand up to the size of the earth, say, we have a mixture of the two, and that this mixture is expressed by Newton’s equation. Newton’s equation is not only a gravitational equation, it is a compound, and it includes both fields. In fact, it is a differential field, meaning you take the gravitational field (the expansion field) and subtract the E/M field from it, obtaining the unified field. This unified field is expressed directly by Newton’s famous equation, without any further tinkering. It takes some tinkering to tease the separate equations out of Newton’s equation, but no effort at all to get unified numbers directly. Expansion provides an apparent attraction, the E/M field provides a real repulsion, and the two together give us what we see and measure with our current equations, a compound field.
I showed this with the earth, providing us for the first time with real numbers for each field. The number 9.8, for instance, is shown to be a number for the unified field. The actual gravitational field is 9.81, and the E/M field is -.01. This means at the level of size of the earth, the gravitational field is more than 1000 times stronger than the E/M field. But this ratio drops off drastically. With the moon I showed that the gravitational field is 2.67 and the E/M field is -1.05. The E/M field is already almost half the size of the gravitational field.** The radius changed by only a factor of 4, but the comparative strength of the fields changed by a factor of 400. By the time we reach the size of everyday objects like marbles and bowling balls, the E/M field has already overwhelmed the gravitational field. It is not big enough to cause noticeable effects, but it is big enough to outsize gravity in experiments like that of Cavendish. When we are talking about unified forces on the order of 10-10N or 10-7N, most of that is going to be E/M force.
You will say, prove it. Well, I have already proved it mathematically in my unified field paper and other papers. I have shown that it is consistent with what we know and explains a lot of things we haven’t known until now. But Cavendish also proves it. Neither Cavendish nor anyone else can explain why so much seemingly important mass can be ignored, mass like that of the walls. I can explain it.
But first I must explain how a repulsive force can cause attraction. In explaining one, I will explain the other as well. What we see in Cavendish is an attraction. But I have just claimed that the E/M field is the dominant field by far at this level of size and that this field is always repulsive. How do I explain this contradiction? The explanation is that we are not seeing or measuring a force between the balls, as has always been assumed. We are not measuring or seeing gravity, in the main. The larger ball or object is mainly a blocker. It is a masking agent. We are not seeing an attraction; we are seeing the blocking of a repulsion [I assure you this is not LeSage's theory or push gravity or Majorana, so read on, please].
What we have is a large repulsive field created by all the external and ignored masses in the vicinity, whether those masses are walls, people, cameras, other equipment, buildings, and so on. All those objects are emitting this repulsive field, composed of photons. Our little hanging balls are being bombarded from all directions by this field. Variations in this field are what cause the little balls to remain in constant motion. They are hanging in a sea of radiation, and this sea is never completely still or balanced itself.
What we do when we set up this experiment is we try to get the torsion arm to quit moving, so that we can add the large balls and begin the experiment. We need an initial stasis, and this is achieved by balancing all the external masses. Rather than measure all those masses and compute the correct position for our apparatus, we proceed by trial and error. If our little balls are swinging wildly, we move them away from this wall or toward that one, or rotate them toward one corner, or go to another location that seems more stable, based mostly on instinct. Once we reach this position, we think, aha, I have blocked all external effects, or gotten far enough away from them that they are negligible. But this is not in fact what we have done. No, we have, by trial and error, reached a point where all the repulsions balance, or nearly balance.
In a world mediated by gravitational attractions of the sort Cavendish envisioned, and that the standard model accepts, this position of balance would be very difficult to find, by either computation or trial and error. Because it is an inverse square field, the field is changing quickly over very short distances, making a walk-about trial and error sort of repositioning all but impossible. But in a repulsion field created by E/M, there is no inverse square law. It is inverse square only if you are dealing with spherical fields, but we are not. And it is inverse quad only if you are dealing with both spheres and relativity, but we are not. In Cavendish we are not dealing with either spherical fields or relativity. We don’t have large distances or large velocities, so relativity is moot. And our walls and ceilings and other objects are mainly flat. This means that they will create bombarding fields that do not diminish over short distances. This makes it quite easy to move about with little rigor and still find a point of balance.
Once this point of balance is found, we simply introduce our large “attracting spheres” and await a motion. But this motion is not caused by attraction. It is caused by blocking repulsion. A gravitational field cannot be blocked, but a basic bombarding field can be blocked, no matter what it is made of. Our large ball simply gets in the way of photons being emitted by the walls. Since the smaller ball is no longer being repulsed from that direction, it moves it that direction, appearing to be attracted by the larger ball. It is that simple. A ball that is closer will block photons more effectively, as will a denser ball, as of lead. In this way, mass and distance considerations mirror those of the expectations of gravity. Move the larger ball farther away and it allows more photons to get by it from more directions. Change either its size or its density, and more photons get past it or through it.
Notice that this explanation also takes into account historical experiments that tried to introduce blocking agents, like lead sheets and so on. If the lead ball is already a blocking agent, then these sheets will not change anything, whether they are placed in back or in front of the large ball. I don’t know that anyone ever had the perspicacity to place a sheet behind the large ball (between it and the wall), but even if they had, it would have little effect. Whether in front or behind, you are only doubly blocking what is already being blocked. If anything, the blocking would increase the effect and the motion, something the experimenters were not even looking for. An increase of this sort might be so shocking it would be suppressed. Certainly we have similar evidence of suppression in similar cases.
You will say that the blocking ball must be emitting photons like everything else. It must be repulsing the littler ball, too. True. And if it is lead, then you might think that not even lead walls could produce more photons per square inch than the lead ball. But this is false. You have to do a full analysis. Think of Huygens Principle, for a start. Every point on the wall (no matter what it is made of) will be emitting as a new source. It will be emitting in all directions. So, to start with, the littler ball was receiving radiation from all parts of the wall, not just the part of the wall that is directly behind the large ball. Beyond that, the wall is not emitting just from its surface. The wall is emitting from every particle in it. If the wall is two feet thick, photons are coming from two feet inside the wall as well as from the near surface. Depending on the density of the wall, some of these photons will be blocked. But not all of them. The littler ball is receiving emission from all parts of the wall and all depths of the wall. It is also receiving emission from anything that may be on the other side of the wall, whether it is another wall, a house, or a mountain. Any radiation that has not been deflected will add to the total.
So you can see that even if our large blocking ball is lead, it is still going to block more emission than it emits. Our big lead ball may be dense, but it has a rather small diameter, compared to the wall. Another way to see this clearly is to look at the large ball from the perspective of the small one. Say the large ball has a diameter of 12”. It will be emitting from a volume less than one cubic foot, and it will be blocking some of its own emissions (the front half of the ball will block some of the emission of the back half). But now put yourself inside the littler ball. Open a peephole and look out at the big ball. How much of the far wall is invisible to you from there? If the big ball is very close, you may not be able to see that wall at all. If the big ball is exceedingly close, you may not even be able to see parts of the ceiling and floor and side walls. Well, everything you can’t see is being blocked. Everything in that cone of sight, all the way back, through the depth of the wall, to the house behind it and the mountain behind that, is being blocked. No matter how dense the big ball is, it can’t be emitting enough to make up for what it is blocking. The denser it is, the more it emits, but the denser it is, the more it blocks. It is always going to block more than it emits. If it does so, then the little ball is repulsed less in that direction than in all other directions, and so it moves that way.
This is why the apple also works, even when you think its mass might not be enough to affect the little ball gravitationally. Notice that the apple has a lot of volume. It blocks a huge swath of emission. It has a low density, so it doesn’t block nearly as efficiently as the lead ball, but for the same reason, it doesn’t emit nearly as much itself. The important thing is that it blocks more than it emits, causing the appearance of attraction.
Now we can go back to gravity, and add that effect to the larger effect we just found. I have shown that the E/M effect is the primary one, but I am not saying it is now the only one. Newton’s force was and is always a compound force, and so is mine. Both the gravitational field and the E/M field are always at work, at every size level. At the size level of our test balls here, gravity is the smaller fraction, but it still pertains. But in this case, both fields tend to cause the appearance of attraction. The most novel thing about Cavendish is that in his apparatus both fields create the appearance of an attraction. Without gravity, the machine would produce an attraction. Without E/M, the machine would produce an attraction. Therefore we have a compound effect.
It is not a compound effect like we are used to, though. Newton’s equation yields a differential field. This one in the Cavendish experiment is a summed field. In most situations, we subtract the E/M field from the gravitational field, in order to find the field expressed by Newton’s equation, as I showed with the Earth and Moon above. In this case with Cavendish, we add. This is one of the many reasons Cavendish has been misinterpreted, and has remained so difficult to interpret.
We therefore must calculate the relative sizes of the fields for our balls. I have shown that gravity is dependent only on radius (density matters only in E/M, and enters Newton’s equation in that way). This makes it quite easy to find the strength of the field. We simply calculate the small ball as a fraction of the earth.
6,378,000/.0254 = 9.815/a
a1 = 3.91 x 10-8m/s2
F = ma = .732a = 2.86 x 10-8kgm/s2
But using Newton’s equation would give us a total force involved for the big and little ball of
FT = 1.47 x 10-7kgm/s2
a2 = 2 x 10-7m/s2
That last acceleration is found by using only the mass of the smaller ball, since the larger one is fixed. Assuming Cavendish was correct to ignore air resistance, gravity was only 1/5 of his total effect (a1 is 1/5 of a2); 4/5 was provided by blocking the E/M field.
That means we have an E/M force of 1.176 x 10-7kgm/s2 acting on the small ball. We will label that T.
T = 4FT/5
But that is a resultant force, the amount of force being blocked plus the E/M force between the balls. What is the E/M force between the balls? From my unified field paper, we find this equation, which is pretty self explanatory.
E = [GMm/R2 ] – [m(A + a)]
If the large ball were free to move, its acceleration due to gravity would be
A = 2.345 x 10-7m/s2
m(A + a) = 2 x 10-7kgm/s2
E = -5.3 x 10-8kgm/s2
So the ball is blocking
B = 1.706 x 10-7kgm/s2
What is the E/M acceleration of the small ball?
aE = E/m = -7.26 x 10-8m/s2
This means that the E/M field is 1.86 times as strong as the gravitational field in this experiment. Which means that, if not for the walls, Cavendish would have found a repulsion!
According to this logic, it should be quite easy to falsify any Cavendish machine in spectacular fashion. But you wouldn’t expect to be able to do it in any room. Someone should take a Cavendish machine (one that is encased) to the top of a mountain, mount it on a very high pole, and then mirror the laser down onto the ground, where it can be read from a distance. If it is a very calm day and your larger lead balls aren’t blown down on your head, you should see the little ball move away from the larger ball. The only reason I can imagine that this would not be true is if the atmosphere somehow reflects and redistributes the E/M field, making it impossible to avoid here on Earth. In that case we would have to take a Cavendish machine into space, drift it out into space a bit, away from the ship, and photograph the motion from a distance. But I predict, rather confidently, that the mountain will provide the reverse effect. An open field might even do it.
Some will say, “Good lord, then a Cavendish machine must be useless as applied to Newton’s equation or theory. We must be getting the wrong number for the density of the Earth and for G.” Not so fast. Remember that I said that Newton’s theory and equation actually includes both gravity and E/M. It always did, even before I came along and noticed it. Newton was not aware of the fields his theory and equation were expressing, but he did express them (nearly) correctly. He got the mechanics and proportionalities nearly correct, since he was taking them from experiment and observation. His equation does express the compound field correctly (minus relativity). Therefore, we can still apply his equation to the Cavendish machine. As you can see, I did apply Newton’s equation, even in my solution.
So the question is, what would we have found without the walls? If I can show that--other than the directional change--we should have expected the same numbers, then I can show that the Cavendish machines’ confirmation of gravity is just a coincidence. In other words, the Cavendish machine may give us a misleading motion, but it may give us almost the right numbers anyway. Without the walls, the set-up would have given us
aE + a = -3.35 x 10-8m/s2
Or a force of -2.45 x 10-8m/s2
This seems too small, but we must remember that Cavendish has been misinterpreted. History has assumed that all the gravitational force present could be expressed by his machine, but I have shown that is false. His large balls are fixed, so their accelerations cannot be expressed. They should be subtracted from the total equation. In other words, Newton’s equation can be applied, but it cannot be fully applied, since all the fields it contain are not capable of being expressed. Newton’s equation includes the acceleration of both the small ball and the large ball, but the large ball is not free to accelerate in any fashion in Cavendish. Given the set-up, we cannot give its acceleration to the smaller ball either, as we are accustomed to do with planets and moons and other unconstrained bodies in gravitational situations. I am no longer defining gravity as force at a distance or curvature, I am defining it as real acceleration. The big ball’s acceleration cannot be expressed here. Therefore only ľ of Newton’s equation is capable of expression in this apparatus. The smaller ball’s field can be expressed, due to the continuous motion of the pendulum, as I showed above. And both E/M radiation fields are unaffected and unconstrained by the apparatus. But the acceleration of the large ball cannot be expressed. Therefore, if we want to match our last equation above to the historical assumption, we must add the large ball back in, like this
aE + a + A = 2.01 x 10-7m/s2
If we apply that to the small mass once again, of course we would expect to find
F = 1.47 x 10-7kgm/s2
That, remember, is the normal outcome of the experiment. You may not comprehend the enormity of what just happened, so I will state it another way
m(aE + a + A) = GMm/r2
I remind you that aE is the acceleration of the small ball due to the E/M repulsion between the large and small ball. This means
(aE + a + A) = GM/r2
Since those three accelerations together describe the resultant acceleration of m and its real motion, we can write them as total acceleration, aT
G = aT r2/M
F = GMm/r2 = aT m
That little diversion should help you understand what G really is, and how both acceleration and E/M fit into Newton’s equation.
To sum up that last series of equations, the problem is that in the Cavendish experiment, he was missing (mA) amount of force. The acceleration of the large ball was never present, never expressed in the motion seen. This is true in all Cavendish-like experiments where the large weight is fixed. So 1.72 x 10-7kgm/s2 of force was missing. But look above: I found that the large ball was blocking B = 1.706 x 10-7kgm/s2
I got those two numbers by completely different methods, but they match almost exactly! Because the ball is blocking that amount of repulsion, we can add it back in as apparent attraction.
This means that Cavendish succeeded by a compensation of errors. The big ball is blocking almost exactly the amount that is missing from the equations, due to the loss of its own gravitational acceleration. Any Cavendish-like machine with large balls that are fixed would be expected to have the same compensation of errors.
This probably explains the variation in all contemporary measurements of gravity, too, including the most recent. Because the researchers are ignorant of the fields present, and the actual actions of their machines, all of their conclusions are skewed. Beyond that, variations will be caused by differing environments, where fields are slightly denser or sparser, where blocking balls block more or less efficiently, and so on. What is most interesting, though, is not the variance, but the relative lack of variance, and my paper explains that as well. As we saw with the apple versus the lead ball, the way that blocking takes place assures that the gain in blocking always offsets the loss in gravity in almost the same way, despite different objects and set-ups. This assures that we have very small variations, like those we find in modern papers; but it forbids large variations. This curious finding explains why Cavendish and gravity have remained mysterious for so long.
Postscript
Some have seen the blocking here and jumped to the conclusion that my theory has something to do with LeSage or push gravity or Majorana or gravity shielding. I encourage these people to look closer. Neither this paper nor any of my papers has anything to do with LeSage, push gravity, or gravity shielding. Notice that I accept Newton's equation as correct, and add nothing to it: no extra terms. My compound field is all contained within Newton's equation and within the historical F. Unlike LeSage, in my theory gravity is still there, expressed not by a bombarding field but by simple acceleration. It is the E.M foundational field that is blocked or shielded here, not gravity. Look above: gravity is never shielded or absorbed or expressed as an emitted or bombarding field. The reason the large object's gravitational acceleration is not expressed in Cavendish is not due to shielding; it is due to the fact that the large object is fixed. It is not free to move. And, although I have two fields like Majorana, expressed as a differential, my second field is not a mathematical addition to Newton or to F. Both of my fields are contained by Newton's equation, which means my equations and theory show no variance from Newton, except in exceptional circumstances like this. Majorana's equation showed variance in all situations, since it included a term for density that was in addition to F. If you study my UFT paper, you see that my density term is interior to F. My density is a part of the E/M field, which is a part of the compound field. This assures that my equations show and predict no variance from Newton in normal circumstances (except variations due to Relativity, which I accept).
*This is now accepted by most everyone, even those who scoff at an expansion theory. Cosmology and gravity specialists now often assume a sort of “space pressure” to explain the force-bearing characteristics of matter, or other subtleties. As I have said elsewhere, it is much more logical and consistent to give pressure to matter than to space. But mathematically, force-in is equal to force-out, so the two theories are not finally incompatible or exclusive.
**These numbers have to be interpreted further, something I don’t have time for here. See tide2.html for a longer exposition.
^http://www.alphysics.com/cavendishexperiment/OntheCavendishExperiment1.pdf
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.