|
return to homepage
return
to updates
New
Energy & Mass
Transforms in
Special
Relativity:
a
compressed argument
by
Miles Mathis
This paper is
a compression of my
full paper showing that Einstein’s energy and mass
transform equations are flawed. In my long paper on
the mass and energy transforms of relativity, I followed
Einstein’s original derivations in his original papers line by
line, showing precisely where the mathematical errors were.
To exhaustively dig out and solve all these errors took me 41
pages. I believe that history will ultimately forgive
me this length, since I did not say anything that did not need to
be said. However I can understand that this length—and
the inherent difficulty of the subject—made the paper a chore,
to say the least. In my defense I can only say that if the
problem had been an easier one, Einstein would not have mistaken
parts of it—and subsequent physicists would have uncovered his
mistakes before me. My longest suit may be tenacity;
and the tenacious, when clearing up errors, do not like to stop
until they are finished.
All that being said, I have fielded questions for some months and
I can now see that a gloss is necessary. It would be
useful to have a short argument, one that moved quickly and was
fairly easy to follow mathematically. Readers with
questions could then refer to sections of the long paper
for clarification. Readers who fully understood and
accepted the short argument could perhaps dispense with whole
sections of the long paper.
Let me start by
reminding the reader that by making a couple of small corrections
in Einstein’s derivation, I was able to derive the classical
energy equation from Einstein’s own equations. That is, I
showed that
K = κmrc2
– mrc2
= mv2/2
In short, I derived a
new transformation term kappa
to replace gamma.
I did not pull this term out of thin air or manufacture it from
theory or philosophy. I achieved it directly by making
simple algebraic corrections to Einstein’s paper of 1905.
This new term elegantly showed the equivalence of Einstein’s
math and Newton’s, as regards kinetic energy.
One final remark before
I proceed. I want to stress once again that deriving the
classical energy equation from Einstein’s postulates and math
does not falsify the major findings of relativity or suggest that
science should return to Newton. Relativity is true.
Distance, time, velocity, mass, momentum and energy all require
transforms from one observer to another. Beyond this,
Einstein was correct in his other postulates, such as the
fundamental postulate of energy transformation—that energy and
mass are equivalent and transferable. My corrections will
actually have a greater impact on the math and theory of General
Relativity. The basic theory of Special Relativity—that
is, relativity caused by velocity—has not been greatly altered
by my corrections; only the math is changed, and, for the most
part, subtly.
Nor is my resuscitation of mv2/2
to be understood as a return to Newton. Newton’s equation
is not a transform and does not allow us to go from measurement
by a object to measurement by an observer. The variables in
Newton’s equations are all as measured by the observer.
They are therefore not relativistic and are useless as
transforms. I only mean to show the true mathematical link
from classical kinetic energy to relativistic. A simple
correction to Einstein’s math shows why Newton’s equation
worked and continues to work in the proper situations. And,
perhaps most importantly, this new derivation shows that c is not
a limit where mass goes to infinity. Since Einstein's equation is
not an infinite series expansion of Newton's, c is no longer a
limit in the math. In other words, my proof below shows that
gamma
is incorrect, which means that
there is no power series or infinite terms, which means that c is
not a mass limit. Einstein's equation and Newton's equation are
mathematically equivalent, and one does not "approximate"
the other. This solves the so-called mass gap in Yang-Mills,
among many other things.
Part
One
Locating the Errors
We will start
with Einstein’s second major paper of 1905, Does the Inertia
of a Body Depend upon its Energy Content? In this
paper he has a body at rest emit two planes of light in opposite
directions. The two planes of light have equal energies;
therefore the body remains at rest after the emission. He
then asks how the energy of this body before and after the
emission would look to an observer moving directly away from the
body at velocity v. Einstein lets the two planes of
light emit from the body at angles to the x-axis and therefore to
the observer.
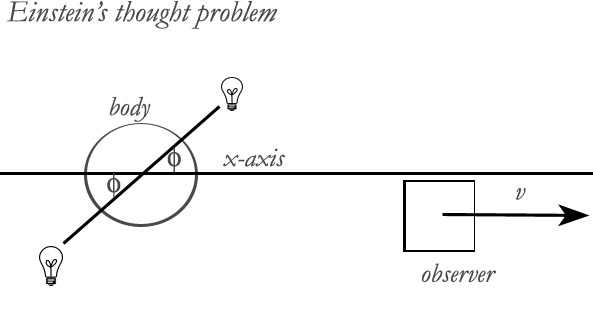
Let
us call B the system of the observer and A the system of the
body.
Using his nomenclature,
E0 = the initial energy in A.
E1 = the energy in A after the emission of the two
planes of light.
H0
= the initial energy of the body as seen from B. That is,
it is the initial rest energy plus the kinetic energy.
H1 = the final total energy of the body from B, being
the final rest energy plus the final kinetic energy.
L/2 = the energy of each plane of light, as measured from A.
E0
= E1 + L/2 + L/2 This is
the equation as calculated from A
H0 = H1
+ aL/2 + bL/2
This is the equation from B, where a is the negative angle
transform and b is the positive angle transform
a
= γ[1 + (v/c)cosφ]
b = γ[1
- (v/c)cosφ]
where γ = gamma
=1/√[1 - (v2/c2)]
Now, Einstein says the initial kinetic energy of the body is
represented by the equation
K0 = H0
- E0
And the final kinetic
energy is represented by
K1 = H1 –
E1
So that the change in
kinetic energy is
K0 - K1
= L{
1
- 1} = γL
- L
√[1 - (v2/c2)]
That is the whole paper. It takes up less than three pages
in Annalen der Physik. The cardinal error is
in the final two steps. Einstein mixes up the last line
with the next to the last line, treating them as the same thing.
But one expresses the final kinetic energy and the other
expresses the change in kinetic energy. They are not
the same in this problem, since the body has an initial kinetic
energy. Einstein assigns the term γL to H1 and
the term L to E1. He assumes that H1
is mc2 and E1 is m0c2.
But look back up the series of steps:
L ≠ E1
H1 ≠ γL
This
is because K1 ≠ K0
- K1.
Once you have digested the enormity of that, notice that in the
final step Einstein has subtracted the final kinetic energy from
the initial. This is backwards. It is standard
practice to subtract the initial energy from the final to find a
change in energy. Corrected, the equation should read,
K1
- K0 = L(1 - γ)
If you insert m0c2 into Einstein’s
last equation (as Einstein did later and as history still does)
this implies that L = m0c2.
Not E0 but L.
In the beginning of the problem, E0 is assumed to be
the rest energy of the particle: Einstein and history have
assigned m0c2 to E0.
But according to these equations, L = m0c2.
That is, m0c2
is not the rest energy before or after the emission of the
light, it is the change in rest energy.
It is the energy equivalence of the planes of light.
Another error is made in assigning values to the light angle
transforms a and b. Notice that the magnitudes of a
and b are not equal. The observer in B would therefore
expect Einstein's body to change course, since one of the planes
of light would have more energy than the other, measured from
B. Einstein ignores this. The body must not
change velocity, because then the change in kinetic energy would
be due to that velocity change and not to a change in mass—which
is of course what he is trying to prove. By a mathematical
trick Einstein gets the two planes of light to add to unity in
both systems, but in B the two light planes do not have equal
energies.
Also, just as in his first paper on Special Relativity, Einstein
has failed to assign v to either system A or B. We
are told that B is moving v relative to A. But is v
measured from A or B? We have two possible numbers for
v: B rel A measured from A, or B rel A measured from B.
Kinetic energy can also be calculated from either system, A or
B. If A can calculate a velocity relative to B, then A can
also calculate a kinetic energy. Einstein does not specify
where K is measured from. The form of the equations implies
that K is measured from B, but this is not a necessity.
The fact that Einstein does not carry into this problem a v’,
as I do, has had long-reaching consequences.
And finally, gamma is not the transform to use here.
Even if gamma had been correct as a transform for distance
and time in Special Relativity, Einstein still should not have
applied it to the light rays here. Physics already had a
transform for frequency that had nothing to do with Special
Relativity, and that should be applicable in this problem.
This transform is f’ = f(1 + v/c). Relativity has not
overwritten or jettisoned this transform; Richard Feynman
actually used it much later as part of his proof of Relativity.*
That is, he uses the correct transform to derive the incorrect
one. Current theory is built on a simultaneous and
inconsistent use of both transforms.
Part
Two
the
Corrections
Now let us
correct these errors. We will have to change the thought
experiment a bit in order to produce all the clear and definable
variables we need. Let us start with the body and the
observer both at rest together. Let us have the body emit
only one light ray in one direction, and let us limit this ray to
a single photon. What difference will this make?
Einstein rigged his math so that his body did not change position
in system A or velocity in B. Our new body, however,
does change velocity. It goes from rest to a final velocity
of v’ as measured from itself in A, or from rest to v measured
from the observer in B. Einstein’s two planes of light
cancel out. My one photon has no twin in the opposite
direction, therefore our body is given a push and it achieves a
velocity.
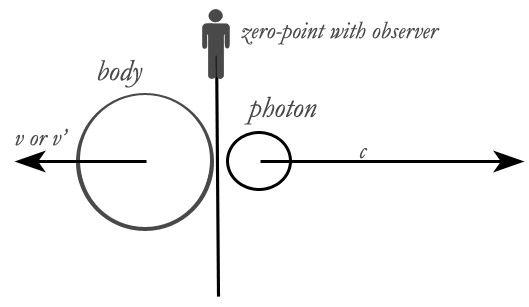
It
is true that this new thought problem implies an acceleration
over an interval, but we can get around that by using an average
velocity over that interval. Let us first relist our
variables, using Einstein’s as a guide.
E0 = initial energy
of the body (measured by the body) before emission of the
photon.
E1 =
total energy of the body measured by the body after the emission
of the photon.
H0 =
initial total energy of the body as seen from the observer.
H1 = final total
energy of the body as seen from the observer.
F0 = energy of the photon as measured by the
body
F1 =
energy of the photon as measured by the observer
α = light
frequency transform
F1 = αF0
since F1 > F0
E1 = E0
- F0
H1 = H0 - F1
E0 = H0 since
the body is initially at rest in both systems, A and B
H1
– H0 = -F1 = -αF0
And
the final kinetic energy is represented by
K = H1
– E1
= H1 –
(E0 - F0)
= H1
– (H0 - F0)
= -αF0 + F0
K =
(1 – α)F0
Now
that I have brought Einstein’s problem into line with my own
thought problem, I may use F1 as the energy of my
photon. Furthermore, I may assume that F1
= m0c2. If we assume that
light can have a mass equivalence, then from the equation for the
momentum of light we have
E/c = m0v
E =
m0c2
where m0 is the mass equivalence of the light.
[Notice that I am accepting Einstein’s postulates concerning
mass and energy equivalence; I am simply not accepting his math.
To achieve E = m0c2 we do not
need any of Einstein’s math; we only need the momentum equation
for light and the postulate that light has a mass
equivalence—both of which Einstein explicitly accepted.]
In order to proceed, we
need an equation for α. My new thought problem shows us
that we need two measurements of mass and two measurements of
velocity. That means we need two more variables than
Einstein worked with. We need m, m’, v, and v’.
This is the only possible way we can do logical mass and velocity
transforms. I must import the equations for v and v’ from
my first paper on Special Relativity. I will include here a
gloss of the math I used to achieve them. In these
equations, primed variables are as observed by A (the object
itself); unprimed variables are as observed by B (the observer).
A simple correction to Einstein’s parameters gives us
xt = x’t’
v =
x'/t = x/t' ≠ x/t
v’ = x’/t’
The reason v ≠ x/t is
that these unprimed variables must be defined as variables as
observed by B, not in B. To say that
another way, x is how x’ looks to the observer. It is
not how the observer sees his own distances. This is a
huge difference, and it is the main problem of Einstein’s and
Lorentz’s original variable assignments. The variable x
is a distance in A observed by B. It is not a
distance in B observed by B. You must understand this fully
before you can proceed with any of my corrections.
t = t'
+ (x'/c)
= t' + (v't'/c) = t' (1 + v'/c) =
t'/( 1 - v/c)
v = x'/[t'(1 + v'/c)]
v =
v'
1
+ (v'/c)
v' =
v =
α v
1 - (v/c)
α = alpha = 1/[1- (v/c)] = 1 + (v'/c) =
c/(c - v) = (c + v')/c
Alpha is the current term for
light frequency transform, as I said above. I have shown
that it is also the correct term for one-degree velocity
transform, replacing the term gamma in the first part of
Special Relativity.
Now we can continue with our energy transforms. Next we
need mass transform equations. These are as simple to
derive as the velocity transforms. When the body emits the
photon it must recoil, achieving a velocity. This velocity
can be found by using the conservation of momentum—the momentum
of the light must be equal to the momentum of the ball:
mvav
= m’vav’ = E/c = m0c
m = m0c/vav
m0
= m(vav /c)
v’av = αvav
= mvav/m’
m = αm’
1/α =1 –
(2vav/c)
We assume a constant acceleration over the
interval in question, so that the average velocity must be half
the final velocity, so
vav/c = [1 –
(1/α)]/2
mvav/c = [m – (m/α)]/2
m0
= (m – m’)/2
And from above we had these equations:
K
= (1 - α)F0
F0 = m0c2/α
K
= -(v/c)m0c2
So now we have almost enough to solve. But remember that m0
is not the rest mass of our body in question; it is the mass
equivalence of the emitted photon. We need to solve in terms of
the body's mass, not the photon's mass. To do this, we need
another mass variable beyond the ones above. It turns out that
there are several variations of mass increase and decrease, and
the equations vary a bit depending on whether the bodies are
emitting or absorbing and whether they are moving toward or away
from an observer. You will have to consult my longer paper
to see why this is so. But you may notice that in Einstein’s
thought problem, the body would be measuring the normal frequency
of light and the observer would be measuring a redshift.
His observer is moving away from the point of emission. But
in my thought problem, the observer is at the point of emission
already. It is the body that measures the redshift.
By
definition–both mine and Einstein's–the rest mass of the body
is the moving mass minus the mass equivalence gained by moving.
In this problem, the mass equivalence gained by moving can only
be the mass equivalence of the ejected photon. What the
body lost in the photon it gained in movement. But we
have two moving masses, m and m’. We also have two
possible mass equivalences for the photon, since A and B will get
different numbers for its energy (F0 and F1).
We must choose m’ since it is connected to v’, which is the
correct velocity (I have shown that v and m, although calculable,
are not correct since they have been skewed by c).
Likewise, we must choose F1 since it is connected to
the normal frequency of light. It gives us the correct mass
equivalence of the light. I have defined the normal
frequency of light as the frequency measured from any point at
rest relative to the point of emission.
mr =
m’ - m0
m0 = [m – (mr +
m0)]/2
3m0 = m – mr
K
= -(m – mr)(v/3c)c2
-3cK/v
= mc2 – mrc2
express mr in terms of m
mc2
– m[1 – (3v/2c)]c2 = -3cK/v
multiply both sides by v2/c2
mv2
– m[1 – (3v/2c)]v2 = -3Kv/c
(3v/2c)]mv2 = -3Kv/c
K = -
mv2/2
The kinetic energy is negative in my problem because the body is
moving away from the observer. It can do no possible work
on the observer.
Once Einstein’s variable
assignments are corrected it turns out that the classical
equation is precisely correct, meaning that it gives us exactly
the same numbers that relativistic equations give us.
Einstein and current wisdom both treat the classical equation as
an approximation at slow speeds relative to c. As
supposed proof of this, they expand the square root in gamma
using the binomial expansion, the first uncancelled term being
v2/2c2. But this is once again
a fortuitous collision of luck and bad math. I have shown
that gamma is an incorrect transformation term, so that
expanding the square root of the term is pointless.
If there is no gamma, there can be no expansion of the
square root and no proof of the approximation of mv2/2.
Besides, this expansion proposes to find that
K ≈ mrv2/2
Which
is absurd. What should have been intended is to show that
K
≈ mv2/2 at slow speeds
This latter equation is the classical expression of kinetic
energy. As I have shown, expressing kinetic energy in terms
of a rest mass in a classical equation isn’t even sensible,
once it is understood what the different terms mean. You
can't express kinetic energy in terms of a rest mass, in a
classical equation. The mass variable in Newton's equation must
be a moving mass. The relativistic equation would have to
resolve to either mv2/2 or m’v’2/2
at slow speeds, even if gamma and Einstein’s theory were
correct. Having it resolve to mrv2/2
is just further proof that no one knew what was going on with the
math and the variable assignments.
Now let us derive the
new energy transforms. Above we found that
-3cK/v
= mc2 – mrc2
-K ≠ mc2
– mrc2
Which means that if the
total energy,
ET = K + mrc2
ET ≠ mc2
m’ = m[1 - (2vav/c)]
mr =
m[1 - (2vav/c)] – m(vav/c)
= m[1 - (2vav/c)
– (vav/c)]
mr = m[1 -
(3vav/c)]
beta = β = 1/[1 -
(3vav/c)]
ET =
mrc2 - (v/c)m0c2
= mc2/β - (v/2c)c2 [m – (m/α)]
= mc2/β -
(v/2c)[mc2 – (mc2/α =
mc2[(1/β) - (v/2c) + (v/2αc)]
ET = mc2[1
– (3v/2c) – (v2/2c2)]
Now
let us find ET in terms of mr, so that we
can compare the transform to gamma.
ET
= mrc2 - (v/c)m0c2
mr
= m’ - m0
m0 = mrβ/α
- mr
ET = mrc2
- {mr(v/c)c2[(β/α) – 1}
= mrc2 - {mr(v/c)c2[v/(2c
– 3v)
ET = mrc2{1
– [v2/(2c2– 3cv)]}
K
= mrc2{1 –
[v2/(2c2– 3cv)]}
– mrc2
The
transformation term here is 1 – [v2/(2c2–
3cv)], which is not gamma. In my long paper I
show that there are several variations of this transformation
term. For example, the solution to Einstein’s original
thought problem gives us the transformation term 1 +
[v2/(2c2– 3cv)], which is also not
gamma. A body moving toward an observer would
have the term 1 + [v2/(2c2 +
cv)].
In my
long paper I showed that Einstein’s own thought problem also
resolved to the classical equation. All the various
problems I solved resolved to K = ±mv2/2.
Amazingly, this was the one constant, no matter what variations
of energy transformation I was dealing with.
Part
Three
The
Accelerator
Why 108?
Let us
now apply our equations to a real experimental situation—the
accelerator. To do this we must reverse the situation of
our thought experiment above—where a body at rest emitted a
photon—and ask what would happen if the body instead absorbed a
photon. Let us call our body a proton, so that we can
assign it a known rest mass (mr
=1.67 x 10-27kg).
We know from experiment that the mass of the proton hits a limit
at 108mr.
We imagine this means that the proton in the accelerator is
accelerating by absorbing energy from the acceleration field.
To see what I mean by this, notice that both my emission problem
and Einstein’s various thought problems all imply that when a
body emits a photon, it not only gains an acceleration from the
emission, it also loses mass or mass equivalence by losing the
“body” of the photon. In other words, the photon leaves
a hole. The rest mass of the body decreases after the
emission. That is what Einstein’s variable assignments
tell us (E1
= E0
- F0).
This would be expected, since a body can hardly emit a smaller
body, no matter whether that body is a particle of light or not,
and expect to keep the same amount of rest energy.
This means that if we reverse the process, the body must gain an
acceleration and gain rest mass from the absorbed photon.
It gains a sort of double energy increase. Let us use our
math from previous papers to express this.
In a real accelerator, the proton is taken to speed in a series
of accelerations. This is an experimental concern, however,
not a mathematical concern. Scientists do not use one
super-field to accelerate since they 1) cannot create it, 2)
cannot keep it from destroying the proton if they did create it.
But we can simplify the math by allowing ourselves to imagine a
super-high frequency photon with which we will bombard our proton
in a single go. The proton will absorb this giant photon
and we will see if the math we achieve from this absorption can
explain the number 108. If it can, then we will have taken
a decisive step in proving these corrections to Special
Relativity. No one has yet been able to derive this number,
and there is currently no theory to explain why there is a
limit. The accepted term gamma implies an infinite mass
increase capability; nor has the math of quantum theory predicted
the existence of a limit or the number 108.
First we must
once again differentiate between our different masses and
mass-equivalences.
m0
= mass equivalence of the
photon
mri
= rest mass of proton before
absorption = 1.67 x 10-27kg
mrf
= rest mass of proton after
absorption, measured from B
m = moving mass of proton,
measured by an observer
m’ = moving mass of proton, measured
by the proton, relative to the observer
By the
conservation of momentum, the momentum of the proton+photon after
the absorption must equal the momentum of the photon before.
mv/2 = E/c [remember that we must use the
average velocity]
E = m0c2
m = 2m0c/v
m0
= mv/2c
1/α =1 –
(v/c)
v/c = 1 – (1/α)
mv/c = m – m’
m0
= (m – m’)/2
mrf
= mri
+ m0
m’
= mri
+ 2m0
m’
= mrf
- m0
+ 2m0
= mrf
+ m0
m/α
= mrf
+ m0
= mrf
+ mv/2c
mrf
= m[1 –
(3v/2c)]
Still the term beta. But let us find m in terms of mri
and mri
in terms of m0.
m/α
= mri
+ mv/c
mri
= m[1 – (2v/c)]
m0
= mv/2c
mri
= 2m0[(c/v)
– 2]
So we only need to return to Einstein’s equations
to make the proper corrections.
E0
= the initial energy of the
proton before absorption of the photon (A as background).
E1
= the total energy of the
proton after the absorption of the photon (A)
H0
= the initial total energy of
the proton as seen from the zero-point (B)
H1
= the final total energy of
the proton as seen from the zero-point (B)
F0
= the energy of the photon in
A
F1
= the energy of the photon in
B
F1
= F0α
since F1
> F0
E1
= E0
+ F0
H1
= H0
+ F1
E0
= H0
since the proton is initially
at rest in both systems, A and B
H1
– H0
= F1
= αF0
And
the final kinetic energy is represented by
K = H1
– E1
= H1
– (E0
+ F0)
= H1
– (H0
+ F0)
= αF0
- F0
= (α - 1)F0
= (v/c)F1
K
= (v/c)m0c2
m0
= (m – m’)/2
mri
= m’ - 2m0
m0
= [m – (mri
+ 2m0)]/2
4m0
= m – mri
K
= (m – mri)(v/4c)c2
4cK/v
= mc2 – mric2
K ≠ mc2
– mric2
4cK/v = mc2
– mric2
mc2
– m[1 –
(2v/c)]c2
= 4cK/v
multiply both sides by v2/c2
mv2
– m[1 –
(2v/c)]v2
= 4Kv/c
(2v/c)]mv2
= 4Kv/c
K =
mv2/2
Which means that if
ET
= K + mrfc2
mrf
= mri
+ m0
ET
= K + mric2
+ m0c2
ET
= mric2[1
+ (v’/2c)]
[1 – (v’2/c2)]
ET
= mric2{1
+ [(v2
+ cv)/(2c2–
4cv)]}
ET
= mc2
[1 – (3v/2c) + (v2/2c2)]
ET
= mc2
[1 + (v’/2c)]
[1 + (2v’/c) + (v’2/c2)]
Notice
the last bolded equation above tells us why gamma
works so well in accelerators
despite being slightly incorrect and being derived with so many
mistakes.
In accelerators we are finding a limit at 108.
Therefore, we set my equation equal to 108 and see what velocity
the proton is really achieving.
(v/c)m0c2
+ m0c2
+ mric2
= 108ric2
(v/c)m0c2
+ m0c2
= 107mric2
This last step was allowed since mri
is the same in both
theories.
[(v/c) + 1]m0
= 107mri
mri
= 2m0[(c/v)
– 2]
[(v/c) + 1]/[(c/v) - 2] = 214
v = .4982558c
c = 2.99792458 x 108m/s
v’ =
.9930474c = 2.97708 x 108m/s
According to current theory, gamma
is equal to 108 at v =
.999957c. The v variable in gamma
is equivalent to my v’,
since current theory has no v’, and since I have defined my v’
as the true velocity of the object.
So, we now have all
our numbers in hand. How am I going to explain the number
108? Notice that we have an unexplained velocity
differential in both current theory and my theory. By
current theory the limit in velocity for the proton is 1.2 x
104m/s
less than c. By my theory the gap is a bit larger: 2.1 x
106m/s.
What causes this gap? And which gap is correct? If I
can answer these questions, then I can show where the number 108
comes from.
Let’s say
that the proton already has a velocity or velocity equivalent due
to some motion or force or other unexplained phenomenon.
Let’s say that the proton’s total velocity cannot exceed c,
and that this other unexplained motion or force makes up the
difference.
That is precisely what I have done in my paper on the Universal
Gravitational Constant. Using a hint of Maxwell and the
dimensions of G, I showed that the proton can be shown to have a
constant acceleration in any direction of 8.88 x 10-12m/s2.
Here is a gloss of that math. Given two equal spheres of
radius r touching at a point, we have
F = Gmm/(2r)2
ma
= 2Gmm/(2r)2
a = 2Gm/4r2
a/2 =
2Δr/2Δt2
We now let the spheres expand at a constant and equal rate.
We assign Δr to a change in the radius instead of a change in
the distance between the spheres, and this allows us to calculate
even when the spheres are touching.
Δr/Δt2
= Gm/r2
After time Δt, the radius will be r + Δr. After any
appreciable amount of time, r will be negligible in relation to
Δr, so that Δr ≈ r + Δr
m = Δr3/GΔt2
a
= 2Δr/Δt2
a
= 2mG/Δr2
That
is the acceleration of each of two equal masses in a
gravitational situation. But if we want to give all the
acceleration to one of them, holding the other one steady for
experimental purposes, then we simply double the value.
a =
4mG/Δr2
If the proton has a radius of 10-13m,
this yields
a = 8.88 x 10-12m/s2
If we allow the proton to accelerate at this pace over its entire
lifetime up until the current moment, then we can achieve a
number for its present velocity due to mass. My velocity is
a much better fit.
Using this acceleration due to mass and gamma,
we get an age of the proton of only 85 million years.
v = at/2
= 2
x 1.2 x 104m/s
= 85 million
years
8.88 x 10-12m/s2
My corrected numbers give an age of the proton of about 15
billion years.
v = at/2 = (8.88 x 10-12m/s2
)(4.73 x 1017s)/2
= 2.1 x 106m/s
My number is therefore a match to current estimates, as you see.
Current theory based on gamma
is clearly wrong, since the
proton cannot be as young as 85 million years. That would
make protons 50x younger than the earth.
[To see a shorter
way to derive the number 108, you may now visit my more recent
paper called Redefining
the Photon. There, I use the density of the charge field to
calculate the number.]
Conclusion
My
mathematical connection of this paper with my other papers on
mass and gravity does several very important things.
1)
I have explained the velocity limit of the proton in the
accelerator. It cannot achieve c due to its mass.
This was assumed by all. But I have shown precisely how and
why the mass limits the velocity. Mass is the acceleration
of a volume. Mass therefore has a calculable velocity over
any interval.
2) The mass has a calculable
velocity equivalent and I have provided the math to achieve this
velocity. In doing so I have dismissed the mass dimension
altogether, showing that mass can and must be expressed with the
dimensions of length and time. I have given the
dimensions of G to the mass, so that G is now just a number.
This means that the kilogram must be redefined in terms of the
meter and the second.
3) I have provided further mathematical
proof of my corrections to Special Relativity. I have shown
one more instance in which gamma fails to give us correct
numbers. Findings in particle accelerators could not
be tied to other theory for two reasons: we didn’t have the
correct theory to tie it to, and we didn’t have the correct
velocity of the particle. My corrections from both ends
allow us to tie up in the middle in a very satisfying way.
4)
The explaining of mass as motion is a huge step in the quest for
a unification theory. One important implication of my new
theory is explaining why gravity doesn’t seem to exist at the
atomic level. It doesn't seem to exist simply because we
have assigned the motion to another "field" or cause.
At the atomic level we have decided to call this force "charge",
but it is the same force as gravity, it is just hiding under
another name. But at both the quantum level and the
macrolevel, gravity is not a force at all.
According to the new theory, you can assign mass, gravity,
charge, strong force, and inertia all to the same basic motion.
All these concepts are not separate ideas, they are different
expressions of the same thing. And they all resolve to
length over time. These last claims were not proved in my long
paper, much less here, but they are proved in links to other
papers, and my mass increase paper is one of the central pillars
in that proof.
*Feynman
Lectures on Gravitation, eq. 7.2.1
If this paper
was useful to you in any way, please consider donating a dollar
(or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me
to continue writing these "unpublishable" things. Don't
be confused by paying Melisa Smith--that is just one of my many
noms de plume. If you are a Paypal user, there is no fee;
so it might be worth your while to become one. Otherwise they
will rob us 33 cents for each transaction.
|