return to homepage ANOTHER HOLE I thought I was pretty good at finding big holes in current theory, but I have to bow to the late Ralph René on this one. I recently read that Mr. René sent simple equations to the National Science Foundation showing that the force on the Moon from the Sun was greater than the force from the Earth. Mr. René claimed that during New Moon, the force was “almost three times as great.”
return to updates
IN CELESTIAL MECHANICS
by Miles Mathis
Well, he was wrong. The force is not greater only during New Moon, it is greater all the time. All we have to do is plug in given numbers for the masses of the three objects and the orbital distances. Using Newton's famous equation F = GMm/r2 we find that the force on the Moon from the Earth is steady all month at about 2 x 1020 N. The force from the Sun varies between about 4.25 x 1020 N and 4.45 x 1020 N. So the Sun's pull on the Moon is always at least 2.1 times as great as the Earth's pull on the Moon. It is almost 2.3 times as much at New Moon (which is not “almost 3”: but I think we can forgive that small hyperbole).
Mr. René tells us he was brushed off with the answer that the Sun is also pulling on the Earth. He complains that in that case, you cannot isolate forces in physics, which would doom all the data in the Solar System and the Universe.
I think we must see that he is correct. We have a real problem here, and the standard-model answer is just one more pathetic dodge. The standard model may even extend its answer to this: “We see Mr. René's point, but what would his solution be? The Moon feels more force from the Sun, therefore it should be orbiting the Sun instead of the Earth? Well, it is. It is orbiting them both. Or, the Moon's primary impulse should be from the Sun, not the Earth? How do we know it isn't? Do we know which orbit the Moon considers primary? Can we decide this?”
I have tried to put the standard-model answer into some kind of logical form, so that we may have something more solid to argue against. But even in this form, it is still very weak. According to all the implications and explications of Newtonian and Einsteinian gravity, a body feeling a greater force from body A and a weaker force from body B should move toward body A. Mr. René has not invented some problem here for his own amusement; he has uncovered a very large hole in field mechanics.
With gravity as the only cause of motions, and with the Sun having more than double the pull on the Moon as the Earth, the Moon should, at the very least, not show such a correctable Earth orbit. Let me show you what I mean by ceding the standard model one of its points. Let us say that Newton's field mechanics can explain the Moon and Earth at the same orbital distance. Since the orbital distance is said to have nothing to do with mass, we only need to let the Moon and Earth have the same orbital velocity. In that case, they can inhabit the same orbit with no problem. Well, in one sense, the Moon and Earth do have the same orbital velocity: they have the same average orbital velocity, since if they didn't, they wouldn't stay together over the span of a year. The Earth has an orbital velocity around the Sun of about 30km/s, and the Moon also has an average orbital velocity around the Sun of about 30km/s.
Problem is, the Moon's orbital velocity, measured relative to the Sun, is highly variable. It varies from about 28 to about 32km/s. (In some cases) it has the slowest speed at New Moon, when it is closest to the Sun. This doubles the problem, because if we could always give the Moon its highest speed relative to the Sun at New Moon, that might almost explain why it was able to resist the extra force from the Sun. But the Moon is often going slowest relative to the Sun when it is closest to the Sun, and that makes it that much harder for the standard model to explain this. To keep the Moon from moving toward the Sun and to keep the Moon's orbit of the Earth from widening at that time, we have to increase the force from the Earth. If we study just those intervals near New Moon, we have to increase the force from the Earth, or the Moon must escape toward the Sun. It must do so NOT because the force from the Sun is greater than the force from the Earth, but because the force from the Sun on the Moon during those intervals is greater than it was during all other intervals of the orbit. The Moon is closer to the Sun, and has less orbital velocity relative to the Sun, so, minus other forces, its Solar orbit must decay.
The only thing in current theory that could prevent the Moon's Solar orbit from decaying at New Moon is the Earth. But the Moon's velocity relative to the Earth over those intervals does not change, since it maintains an orbital velocity of about 1.022km/s all month and all year. Yes, there is some variance in that number, but we do not find that the Moon is always at perigee at New Moon. And even if we did find that to be the case, the eccentricity of the Moon's Earth orbit is not enough to offset this increased pull from the Sun. To protect the Moon from the Sun at New Moon, the Earth would have to hug the Moon quite closely each and every month, and of course it does not do that. If the orbital velocity and orbital radius do not change (dramatically), then the only other cause of stability would be an increased force from the Earth. But according to current equations, the Earth cannot change its force unless it increases its mass. So neither Newton nor Einstein can explain this one.
Mr. René is correct. Even if the Moon and Earth could theoretically inhabit the same orbit, the Moon would have to be pulled lower at New Moon by the Sun. If it were, it could not re-establish its original distance. Once its distance from the Earth had been increased, its pull from the Earth would be lessened, due to the same equation. It would escape very quickly.
To see what I am getting at, let us look more closely at the Full Moon position. The current orbital equation is a = v2/R. By that equation, the centripetal acceleration of the Earth is .006016 m/s2. The centripetal acceleration of the Moon is .006407. The Moon is outside the Earth, but feels more pull from the Sun? That is impossible. The gravity field decreases with increasing distance, remember? That old inverse square law? How and why would the Sun pull more on a body just because that body speeded up? The orbital equation is hiding a huge hole in the field mechanics. In fact, Newton's orbital equation contradicts Newton's gravitational equation. Newton's gravitational equation tells us that the field diminishes by the inverse square, but the orbital equation tells us the field can increase at greater distances simply by increasing the speed of the orbiter!
To make sense, and to create the proper balance relative to the field of the Sun, the Full Moon should always be going slower than the Earth. To see this more clearly, let us get rid of the Moon and just look at the Earth. If we wanted to move the Earth out from the Sun a bit, would we speed it up or slow it down? Well, since logically the field of the Sun should be slightly weaker at greater distances, the orbital velocity should have less centripetal acceleration to offset. So we should slow it down. We can prove this just by looking at Venus and Mercury. Venus is going faster than the Earth and Mercury is going faster than both. Mars is going slower. Here are the numbers: Mercury, 50; Venus, 35; Earth, 30; Mars, 24. Therefore, if the Moon is going faster than the Earth at Full Moon, it cannot be balanced with respect to the Sun. It should escape, just as at New Moon.
I will be told that the Earth keeps it from escaping at Full Moon, but this is to ignore the numbers and the logic of them. The Earth can “offset” only the Moon's velocity relative to the Earth. The Earth cannot offset the Moon's velocity relative to the Sun, because that number belongs to the Sun/Moon motion. This is what Mr. René meant by “isolating forces.” The Earth's field cannot block the Sun's field, short of some revolutionary new hypothesis that no one has yet made. And since that is so, the Moon is just as out-of-balance at Full Moon as it was at New Moon.
Let's look at a diagram, to clarify this. [I had previously published a faulty diagram here. I have corrected it. However, my error does not change the main thesis of this paper. Everything I say above still applies.]
To avoid speeding up and slowing down, you see the Moon would have to stay directly in line with the Sun at all times. It would have to stay on the radial line out from the Sun. This means the Moon would have to orbit precisely in the ecliptic. But we know the lunar orbit is inclined about 5 degrees to the ecliptic, and this is what requires it to speed up and slow down relative to the Sun. Now, we are told it is the eccentricity of the Moon that causes the variation in orbital velocity, but it can't be only that. If the lunar orbit is inclined by any amount, then the Moon must be "getting ahead" of the Earth (relative to the Sun) either at New Moon or Full Moon.
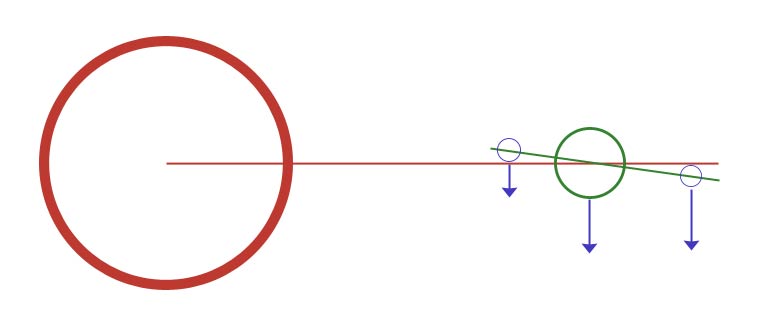
To go from just behind center to just ahead of center, it must speed up its velocity relative to the Sun, as you see. How could it do that, given a gravity only field?
I have already addressed this problem in my celestial mechanics papers, but even I hadn't thought to do these basic calculations, showing the superior force from the Sun at all times. Mr. René's simple calculations just highlight once again how big the problems are for the standard model, and how poor their evasions really are. I had shown that the “innate motions” of the Earth and Moon had to be changing underneath the modern equations, to create this stability; but here we see that the forces are changing in unexplained ways as well.
Of course, contemporary physicists have long since given up talking or worrying about innate motions, and they will answer my new attacks the same way, no doubt. That is, they will retreat into General Relativity, where there are no forces. They will hide behind tensors and claim that Newton's equation is a dinosaur. Unfortunately, it is known by everyone, including them, that Einstein never claimed to have overthrown Newton. Einstein only claimed to have extended Newton's equations by importing time (and therefore mass) differentials into his field. That is, GR is Newton plus SR. And this means that modern physicists have nowhere to hide. Their new field equations do not solve this problem, since motions are still determined by mass interactions. No amount of new math can hide the fact that the Moon is out of balance at New Moon and Full Moon in the three-body problem, no matter whether you try to solve it with Newton's math, Laplace's math, or Einstein's math. All three men could sum the orbit very cleverly, but none of them can explain the differentials.
I have shown that the only way to really answer Mr. René is to take his math seriously, since it is Newton's math, after all. You can only dismiss Mr. René as a crank in this case by dismissing Newton as a crank. I have no intention of dismissing either man as a crank. Fortunately, I have an answer for Mr. René, and my answer is not some kind of dodge. It is the answer I have been giving to all embedded problems in celestial mechanics: the field between all celestial bodies is a two-part or unified field, with both gravity and the foundational E/M field involved in each and every interaction. This solves our current problem because the E/M field changes more quickly than the gravity field, giving us a degree of float. The E/M field changes at 1/R4, which allows it the strength to make this correction we require. I have shown that it is a repulsion, so when the Moon gets nearer the Sun, the Sun repulses it more. By the same token, if the Moon moves away from the Earth, the Earth repulses it less. Therefore, the Moon is balanced by four fields, not two. Every three-body problem is a balancing of six fields, not three. I have shown how this balance is created mathematically in several papers, including my paper on Laplace, my paper on Bode's Law, my paper on Axial Tilt, my paper on the Magnetopause, my paper on Optical Equivalence, and my paper on the orbital distance of Mercury. Therefore I will not repeat the math here.
Another way to look at this problem is to realize that the Solar charge field diminishes as you go out. Therefore, at New Moon the Moon has to travel through a denser solar charge field than at Full Moon. This gives us a field variation we did not have before. We can apply the same logic to the Earth's charge field as well. Since the Moon is in ellipse, it is closer to the Earth in some positions. In those positions, it is traveling through denser charge from the Earth. This gives us a second variation, to help us explain the known anomalies in the lunar orbit. Current lunar theory has measured all the motions of the Moon to amazing tolerances, but it has not fit the measurements to theory with equal exactness. Using gravity only, the motions of the Moon can be listed but not fully explained. It requires a second field to explain all the perturbations we see. It requires my unified field.
Mr. René suspected that the E/M field was the solution to his problem, but he was not able to make the proper corrections to the field. He did, however, state that Coulomb's equation needed work, and he was right about that. I have shown the necessary corrections. Mr. René's basic problem in searching for a solution was that he tended to oversimplify. He saw that the standard model had the opposite problem: terrible over-complication. So he tried to state a simple solution to the field problem. He wanted to replace gravitational attraction with E/M attraction of celestial bodies. In this way, he was paralleling the proposed solution of plasma physicists and the Electrical Universe theorists. All these people are on the right road, but they have not yet found the center stripe. The resonances and perturbations and fine balances of the Solar System cannot be solved with a single field, whether it is gravity or E/M. We require both.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.