return to homepage
return to updates
A CORRECTION
TO THE EQUATION
a = v2/r
(and a Refutation of Newton's
Lemmae VI, VII & VIII)
by Miles Mathis
First written April 2004
Part One
Introduction
It is assumed by most that Einstein's corrections to Newton's gravitational equations all but completed the necessary analysis of the problem. Einstein fine-tuned an already highly successful mathematics, and almost nothing is left to be done. That is current wisdom.
Of course work continues on the mechanism of gravity, since it is still completely unknown. But the mathematics of gravity is considered to be finished. No one is working on the field equations of General Relativity because they are assumed to be correct.
This paper shows that this assumption cannot be maintained. I have uncovered a basic error of math in one of Newton's fundamental equations. The equation, and Newton's derivation of it, has stood unquestioned for centuries. The equation is used today in many esoteric theories, including the derivation of the Schwarzchild radius, the predicted intensity of a gravity wave, and on and on. It is imported into these derivations as a known fact. Furthermore, the equation is used in General Relativity. It is one of the basic preconditions of several parts of various tensors. I show that all these derivations and computations are fatally compromised by this.
The equation is a = v2/r . We all learned this equation in high school, in regard to uniform circular motion. It states the relationship between an orbiting velocity and centripetal acceleration. The reason the equation is used so often in contemporary physics is that it is also assumed to describe the relationship, in its simplest form, between an orbiting body and the force of gravity felt by that body. It is basic physics, and I would guess that no one has looked hard at the equation in a very long time. Certainly no one has had the perspicuity, or the gumption, to question it in a high school physics class. By the time a student of physics reaches college such equations are not interesting anymore—they are outgrown toys—ones to be used if needed, but never closely examined.
I was led to examine this equation due to problems that have cropped up in several fields. I will not get into theory in this paper: suffice it to say that the fundamental concepts of gravity seemed to me a bit attenuated in several areas. What was necessary, in my opinion, was not more esoteric math—as in pursuing superstring theories and the like—but rather a closer look at the theories and concepts that supported gravitational mathematics, and especially the simple algebra that lay under most of the higher math. In doing so, I have discovered many errors that can only be called astonishing, I think. This paper relates one of them.
Part Two
Newton's Derivation
Newton used the equation a = v2/r to tie his famous equation of universal gravitation to Kepler's Third Law. That is,
F = Gm1m2/r2 becomes
t2/r3 = 4π2/Gm2 only by assuming that
a = v2/r
The full derivation is in all college textbooks and I will not repeat it here. I only mention it to show that a = v2/r has been a bedrock equation from the beginning. Newton treated it almost as an axiom himself. He "proved" the equation in a very early part of the Principia (Section 2, Proposition 4). I say "proved" because the equation is actually introduced as a corollary, with only the outline of a proof. Corollary 1 is but one sentence embedded in a theorem. This is corollary 1, in full: "Therefore, since those arcs are as the velocities of the bodies, the centripetal forces are in a ratio compounded of the duplicate ratio of the velocities directly, and of the simple ratio of the radii inversely." In modern English, that is, "Since the arc describes the velocity, the acceleration is the square of the velocity over the radius." Newton might justly reply that his sentence contains no implication of exact equality. He simply said that the force was proportional to the inverse of the radius. Therefore, if the equality is not exact the mistake was never his.
In fact, in the previous paragraph, he had said, "These forces tend to the centers of the circles and are one to another as the versed sines of the least arcs described in equal times; that is, as the squares of the same arcs applied to the diameters of the circles." I read this to mean that, according to the trigonometry applied to the problem, it is the diameters that take the proportionality, in the first instance. Newton then elides from diameter to radius simply by saying, "since the diameters are as the radii." To me this proves beyond a doubt that he is talking in this section of proportionalities, not equalities. Both the radius and the diameter are equally proportional, since proportionality does not take into account first-degree magnitudes. If you are proportional to 2x then you are proportional to x.
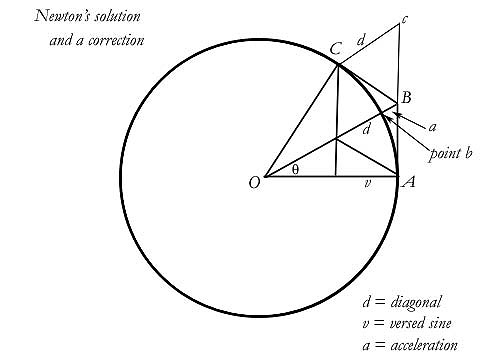
The current derivation of the equation never mentions Newton's method using the versed sine, presumably since knowledge of versed sines is no longer common. Or it may be that the method is not mentioned because it is very difficult to penetrate. I will show that it comes much closer to solving the problem than the current derivation. This should not be too much of a surprise, considering the author. However, by standing on Newton's shoulders modern science should have seen farther eventually, one would have hoped, given the 300 years it has had to perfect his work. Instead it appears that it has only used its time to become myopic, replacing a slightly flawed derivation with one that is a mathematical embarrassment.
Since I prove below that the current derivation fails badly, I feel I must also analyze Newton's original derivation, to show that science does not, at least, have the ignominy of replacing a correct derivation with an incorrect one. Both Newton and the current derivation make fundamental errors in analyzing circular motion.
Newton proposes a body that moves from A to B, is there compelled by a force which turns it, and continues on to C. It had a constant velocity to start with, therefore AB = Bc = BC. Newton postulates that c is where the body would have gone without the force. He seeks the size and direction of the force to turn the body from c to C. He assumes that d is the acceleration vector caused by that force, since it is the difference in the two velocities.
In trigonometry, the versed sine is simply the outer section of the radius, when the radius has been cut by a line dropped from the far end of the arc. Newton never draws this line in his Principia diagrams, which is interesting. Newton liked to hide his math, for whatever reason. It is assumed that the reason was to keep the competition guessing, but in this case it appears to me to be a bit of obfuscation. Hiding good math may be cleverly cloak-and-dagger for some, but hiding bad math is always something less than that. What Newton is hiding may have been clearer in the 17th century, but it is very arcane now. The versed sine approaches zero very fast for very small angles, so that it may take on what is called the sagitta equation:
versine = h2/2r ; (where h = rθ)
Newton proposes that, at the limit, h = the arc. And, since the versine is proportional to the centripetal force, the acceleration must be proportional to arc2/2r. Furthermore, he says, the arc is equal to the velocity, so that a is proportional to v2/2r. But, the versine is only half the force, he says [see Prop. I, Corollary IV], so that the full acceleration becomes a = v2/r. You can see that the sagitta equation is the key to understanding Newton's derivation. Newton gives away none of this in the Principia, but it is the only way to understand his comments on the versed sine.
This is Newton's hidden math, such as it is. It is finessed in several ways, one of which is his use of Lemma VII. In Lemma VII, Newton states that at the limit (when the interval between two points goes to zero), the arc, the chord and the tangent are all equal. But if this is true, then both his diagonal and the versine must be zero. According to Lemma VII, everything goes to either equality or to zero at the limit, which is not helpful in calculating a solution. Neither the versine equation nor the Pythagorean theorem apply when we go to a limit by Newton's definition. I will show below, with a very simple analysis, that the tangent must be allowed to remain greater than the chord at the limit; only then can the problem be solved without contradiction.
Before I do that, it is interesting to note that Newton nearly achieves the correct answer, despite some faulty lemmae. The versine will give us the correct answer, provided we analyze the correct interval. The versine becomes equal to a only if we are considering the arc length from A to b. Newton has been considering the arc length from A to C. We must drop the perpendicular from b instead of C, in order to achieve the correct versine. If we do this, we do indeed find that versine = a at the limit.
Once we have found a in this way, there is no need to double it though, since in finding the versine we used the angle θ and the arc length from A to b. That must therefore be our interval. You may say that the only difference in Newton's method and my correction is that he finds the force over the interval from A to C, whereas I find the force from A to b. His force is twice mine, and his arc is twice mine, therefore everything should stay the same. But it is not quite that simple.
What we find by Newton's method once we discover d, is the force required to move the body from c to C over the interval B to C. I agree that this force is
d = 2a = v2/r
Newton then spreads that force out over the interval from A to C, and we have our current equation. Obviously, the force to take the body from A to C is twice the force to take it from A to b. If I admit that a = v2/2r then I must admit that d = v2/r. I do admit it. But there remains one very big problem. Newton has gone to the limit to find d. I have gone to the limit to find a. We are both supposed to be at the ultimate ratio. I have just shown, however, that he has found the solution over not one but two intervals. He begins Proposition I with this: "For suppose the time to be divided into equal parts, and in the first part of that time let the body by its innate force describe the right line AB. In the second part of that time, the same would proceed directly to c, along the line Bc equal to AB." So he has postulated two time intervals. You cannot postulate two time intervals and then postulate that you are at the ultimate interval. The ultimate interval is the last interval in the series. It cannot be further subdivided, by a time variable or by anything else. Therefore d = v2/r must apply to two time intervals. It is the force required to move the body twice the ultimate arc distance, by Newton's own reasoning.
Perhaps you can already see that it is much more logical simply to let Ab be the ultimate interval, so that the arc Ab is compounded of the vectors AB and Bb. Then we can solve for a using either a versine or the Pythagorean theorem—which is what I do below. In either case we find that over the ultimate interval, a = v2/2r.
I want to highlight one thing before I move on. I quoted Newton above as saying that the arc was the velocity, as derived by his method and by his equations (which still stand today). This means that the variable v in all final equations must be understood to be the orbital velocity. It is not the tangential velocity. The tangential velocity is shown by a straight-line vector along the tangent. That means that it moves in that direction. That is what the vector stands for. The tangential velocity does not curve, and it does not follow the curve of the arc. In the diagram above, the tangential velocity over the first interval is AB and the orbital velocity is Ab. Newton gives us the tangential velocity to start with, when he gives us AB; then we seek the orbital velocity. The velocity that follows the curve of the arc is the orbital velocity, and it is the velocity variable in Newton's final equation a = v2/r. Historically, physicists have not kept these two velocity variables separate, but you must learn to do so as you follow the arguments and diagrams in this paper. The two velocities have become conflated, and when we get to modern equations like v = rω, there is confusion about what v we are talking about. Contemporary textbooks tell us that the v in that equation is tangential velocity, but it isn't. It is orbital velocity.
In further analyzing this problem, I will also prove that the arc does not describe the velocity—or any true velocity—and that we require a further equation to express a in terms of the tangential velocity. The tangential velocity and the orbital velocity are not the same thing—although by Newton's Lemma VII they have been taken for the same thing throughout history. The tangential velocity is the tangent and the orbital velocity is the arc. Lemma VII says that they are the same length at the limit. I will prove that this is false. Beyond that, I would ask you to consider the very elementary fact that an arc is a curve. A curve cannot describe a velocity, since by definition a velocity cannot curve. A curve describes an acceleration, as we all know. The orbital velocity is a velocity only over the ultimate interval—where it becomes straight. But even there it is not equal to the tangential velocity, as I will prove.
It may also be worth pointing out that the basic linear equation for acceleration is v2 = v02 + 2ar. That is in chapter one of most physics books. It took me several years after writing this paper to remember that that reduces to
v2 = 2ar
v2/2r = a
Amazing, really, that no one thought to connect those two equations.
Part Three
The Current Solution
Newton provided a mathematical proof that was both slender and dense, but current textbooks offer a slightly more explicit derivation. What I have copied here is the standard mathematical derivation of a = v2/r. I have taken the steps below from a recent college textbook.
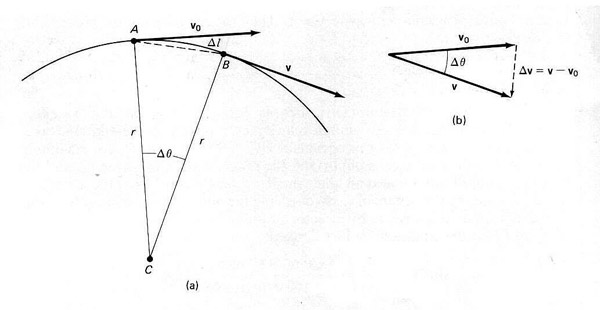
This then is the accepted derivation of a = v2/r:
Let vo be the initial tangential velocity, as shown in the first illustration.
Since vo and v are both perpendicular to r, the two angles θ must be equal; therefore the triangles shown are similar;
therefore as t→0,
Δv/v = Δl/r
Δv = vΔl/r
a = lim Δv
t→0 Δt
= lim vΔl
t→0 rΔt
And since the speed, v, of the object is lim Δl
t→0 Δt
a = v2/r
The book says, "When Δt is very small, Δl and the angles are also very small, so v will be almost parallel to vo, and Δv will be essentially perpendicular to them. Thus Δv points toward the center of the circle."
The mistakes here are many. Disregarding the conceptual setup and the calculus for a moment, let me hit the most important problem first. In its derivation the textbook assumes that the variable v in the last equation is the same as the one in the first. But it's not. In the first line of the derivation, the variable v stands for the tangential velocity. Four lines later we are told "the speed of the object, v, is
lim Δl ."
t→0 Δt
But that is the orbital velocity! The variable v has switched You can see that v in their first diagram is not limΔl/Δt, since limΔl/Δt is the curved velocity from A to B: v is only a component of that velocity; v is a straight line! But the book substitutes one for the other. That is,
vΔl magically becomes v2
rΔt r
But, if v ≠ lim Δl
t→0 Δt
Then the substitution must fail. It does fail, and the derivation falls with it.
A closer analysis of the situation shows that v is the tangential velocity, Δl/Δt is the orbital velocity, and they will never be equal—not over any interval, including an infinitesimal interval. The book needs subscripts to differentiate the two, like vt and vorb (for v orbital).
vorb = Δl/Δt but vt ≠ Δl/Δt
So the equation a = v2/r should read a = vtvorb/r, if the book is following its own method very closely.
vt vorb/r ≠ v2/r.
It is finally unclear whether v in the current equation applies to orbital or tangential velocity, since the derivation makes both assumptions.
For those who are already confused, let me state that in a slightly different manner. This modern derivation is a piece of prestidigitation, or sleight of hand. Like a magician who has crossed over, I will uncover the magic for you. Return to the illustration and notice that they have labelled the two tangential velocities as v0 and v. Why? The two vectors are both tangential velocities, they are just in different positions. But it is the length or numerical values of the vectors we are interested in, not their positions. The numerical values are the same, so the vectors should both be labelled the same. In value, v0 = v, so labelling them differently is just a trick. It is this trick that allows the magicians here to push you from v0 to v, and to complete this dishonest proof. Look again at the equation
Δv/v = Δl/r
Ask yourself, shouldn't that be
Δv/v0 = Δl/r
That is where the switch was made. That is where the hand is quicker than the eye. As you see, v0 has shifted to v, so that when the arc is also defined as v, the two will look the same on the page. Then the magicians can substitute one for the other, and achieve the desired result.
Shocking, really, to find such hamhanded cheating in foundational math and physics.
But there are even more problems. Notice that the magicians allow themselves to make substitutions in a limit equation. I am talking about the equation
a = lim Δv
t→0 Δt
They substitute vΔl/r into that. But you can't do that, because those variables are captured by the limit sign. That equation reads, "The limit as t goes to zero of change in v, etc." That is not the same as simply "change in v." The substitution is disallowed. After the substitution, you see, you have Δl going to the limit, whereas before you had Δv. To make the substitution, you have to assume that the two delta variables go to the limit in the same way, but you cannot assume that. The specific reason you cannot assume it is here is because the two deltas are not equivalent. Δl, like Δt, is a simple interval. But Δv is a change in velocity, which is not a simple interval. A change in velocity is already an acceleration, by definition, which means it is not the same sort of variable that Δl is. In the calculus, you must differentiate lengths and velocities and accelerations, usually by primed variables, but here we have none of that. An acceleration looks just like a length here, with no difference in notation.
And the problems continue. The entire (b) part of the illustration is false. Δv ≠ v - v0, because this math is concerned with values, as I said. The numerical value of v is the same as the numerical value of v0, so Δv could only be zero here. A body in orbit does not change the numerical value of its velocity. It has a constant velocity. The difference between v and v0 is only an angle here. So solving in this way can only be called perverse. Even Newton didn't try to subtract one tangent from another. Look back above at his derivation. He analyzes lengths and velocities and acceleration in the same interval, not in subsequent intervals. The vector v should be no part of this analysis, and using it to manufacture a proof here is just flamboyantly bad math.
Part Four
Feynman's Variation
Some will say that I have simply taken a bad of example of the proof from a poor textbook. To answer this I will provide a different proof from a completely different book. I will critique a proof of the equation by Richard Feynman. Feynman is famous for explaining difficult problems lucidly and concisely, we are told. I take the proof from Six Not-so-Easy Pieces.
Feynman varies the problem a bit, for good measure. This will get us out of our rut, perhaps. He postulates any velocity along a curve, not necessarily a circle.
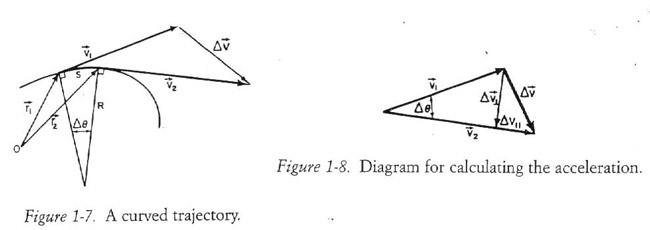
As you can see from his diagrams, the tangential velocity varies and this gives us two components to the acceleration. [In the first diagram, you can ignore the little r vectors and the origin o: they do not really come into this problem. And the vector for Δv is drawn in the wrong place on purpose by Feynman. I will not take him to task for it. He "corrects" it in the second diagram. I do take him to task for that correction.]
He says, "The acceleration tangent to the path is of course just the change in length of the vector." I agree. But I point out that in uniform circular motion this component of the acceleration will be zero, since the length of the vector is not changing. He then calculates the other component, the acceleration at right angles to the curve. You can see the break down in his second illustration. This illustration clears up some of the points left vague in the textbook illustrations. You can see, for one thing, that the right angle made by Δv┴ is where it intersects v2, not v1. He then says that Δv┴ = vΔθ, where "v is the magnitude of the velocity." He does not specify which velocity, but it is clear that he means v1 , since that is the hypotenuse. That is the only way the equation even looks like working, at a glance.
But we already have major problems.
Δv┴ = vθ is a false equation. I hope you can see that it should be
Δv┴ = vsinθ
There is more. Let us say that the tangential acceleration happens to be zero over this interval of the curve. We are back to circular motion in that case. We keep Feynman's second diagram but lose
Δv║. But you can see that makes v2 shorter than v1. Feynman's triangle must be a right triangle for his last equation to work. But the lengths don't add up. v2 - Δv║ ≠ v1 . This means that to calculate a perpendicular acceleration, he must have a negative parallel acceleration. Logically impossible.
Feynman gets into even more trouble. In the next step he lets a┴ = v┴/Δt. That should be a ┴ = vsinθ/Δt. But to get Δθ/Δt, he says, if "at any given moment the curve is approximated as a circle of radius r, then in a time Δt the distance s is of course vΔt where v is the speed." This would give us
Δθ = vΔt/r
Δθ/Δt = v/r
a┴ = v2/r
I hope you can see that he made exactly the same "mistake" in that step as the textbook. You must go back to his first illustration to find s. Once you find it you see that s curves: s is a distance along the arc. He says that
s = vΔt
But this is simply not true. He has already defined v as the magnitude of v1. Therefore vΔt describes a straight line length along that first vector v1—not a length along the curve. He has confused tangential velocity and orbital velocity. His variables have shifted in the same way the textbook's did. Nor does he tell us at the end what v stands for in the final equation. A reader has no idea, since he has defined it both ways.
Furthermore, he has hidden a step previous to Δθ = vΔt/r above. He needs an equation for the arc length s, which would be
Δθ/2π = s/2πr
Δθ = s/r
Notice that this is not the same as sinθ = s/r, therefore the substitution fails. Remember that we had Δv┴ = vsinθ from above. You can see why Feynman suppressed that step. He didn't want it to suffer any scrutiny. Besides, the equation Δθ = s/r only works if θ is measured in radians. But Feynman cannot measure the angle in radians and hope to achieve a solution this way. He wants a velocity measured in m/s, not in radians/s.
Also notice the strange notation for the angle. An angle is usually represented simply by a variable, not by a delta variable. That is, θ not Δθ. An angle is already understood to be a change in direction: the delta is superfluous. But in these derivations both Feynman and the textbook use the delta notation. Why? In order that the derivation seem to work. To trick the eye. Trompe l'oeil. That delta sign makes the variable seem more than it really is. It is a sort of mystification. You look at that the first time and say to yourself, "What does that mean? Δθ? Does it mean something more than θ. I don't know, but maybe Feynman knows. This proof must work, since I already know that a = v2/r, so it is best just to pretend I understand what is going on here." The problem, you now see, is that no one knows what is going on here. The proof is a whitewash.
And finally, notice that Feynman has simply done a copy job on the textbook's ridiculous illustration. Specifically, he has drawn v2 sticking off the far end of the arc. He glibly warns us that vector additions work "only when the tails of the vectors are in the same place" and so he moves the tail of v2 to that of v1. What he forgets to warn himself is that vector additions work only when the vectors are in the same interval. Importing a vector willy-nilly from a subsequent interval just because you need it to finesse an equation is no better than drawing open-tailed vectors or three-headed vectors.
Feynman's proof fails. It fails in at least three places in a half-page derivation.
I am unsure what to think of this, frankly. I truly do not know whether he and everyone else cannot follow short steps of high school geometry or whether there is a conspiracy to hide these errors. It is beyond belief that the greatest minds of the 20th century cannot see these errors. This sequence of steps in Feynman's book is so obviously finessed that it can only mean that it was done purposefully, I think. You may think the arc length equation was left out because everyone knows it by heart. I think it was left out to help hide the unequal substitution of sinθ for Δθ . If Feynman and others like him cannot see these mistakes, it is a very bad sign. If they can, it is a very bad sign, since it means that we are the victims of some sort of Jesuitical casuistry—being lied to for our own benefit. We must believe that science is not another house of cards, lest we run screaming into the night. Therefore we must take these absurd derivations on faith. Credo quia adsurdum. I suspect that this derivation is used simply because it was used by Newton, and we have never been able to improve on it. It yields the correct experimental numbers, so who cares that it is full of holes?
To see my critique of Maxwell's proof of this equation, you can now go here.
To see my critique of an "engineering" proof of this equation at youtube, you can now go here.
Part Five
My Solution
We have seen three different failed derivations, from the likes of Newton and Feynman, no less (although I should probably not put Newton and Feynman in the same sentence). I will not critique Huygens derivation here, since I consider it equivalent to Newton's. He, like Newton, correctly showed the proportionality of the acceleration, the radius and the "velocity." But he did not incontestably show the equality. I will do so now, by a very transparent method.
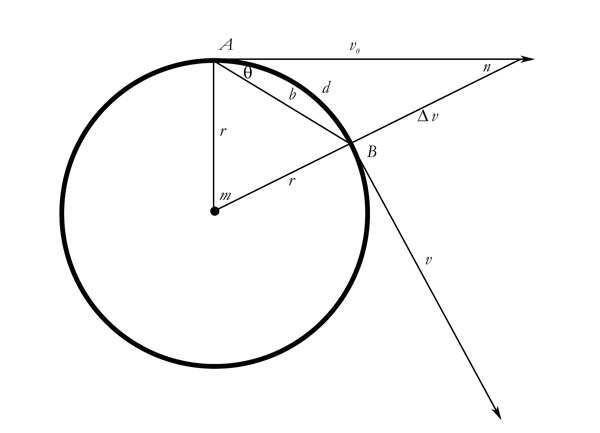
[I have drawn v flying off like that only to mirror the textbook illustration, to show how absurd it really is. In my solution, that vector is superfluous.]
In my drawing, a right triangle is formed by the radius, the tangential velocity, and Δv added to another radius. No matter how short or long you make the tangential velocity vector the right triangle pertains. Also notice that in my illustration Δv is always pointing at the center of the circle. It does not point at the center only when t or Δv or arc d is zero. It points at the center if vo is very long or if it is infinitesimal. Now all we need is the Pythagorean theorem.
vo2 + r2 = (Δv + r)2
Δv2 = vo2 - 2Δvr
To solve, we can then treat that last equation as a quadratic equation, and use the standard method for finding the square root (see your math textbooks).
Δv = a = ±√4r2 + 4vo2) - 2r
2
If we assume a positive motion around the circle, that reduces to
a = √ vo2 + r2) - r
First of all, notice that Δv = a. That vector is the centripetal acceleration. That vector is the number we are seeking. I followed the example of the book and Feynman in putting off a full description of what Δv applies to. Until now. But it is clear that Δv is not a velocity vector. It is an acceleration vector. Of course the form alone should tell us the difference. A delta v vector is not the same as a v vector. A delta v vector is an acceleration vector, clearly. Feynman and the textbook imply that it is the difference between one tangential velocity and the next: a difference between velocities is an acceleration. But I have shown that the acceleration vector Δv can be calculated from a single tangential velocity, given the radius. It is the difference between the tangential velocity and the orbital velocity, measured over the same interval. In this way my analysis mirrors that of Newton, who said the same thing. See above where Newton defines the length d as the difference between the tangential velocity and the orbital velocity, measured over the same interval. My illustration also mirrors his, as you can see. Just flip his illustration over, and his d is my Δv. The only difference is that I point my vector at the center of the circle.
Some will say, "That won't work. You need to differentiate. You need to find your values at a dt. As it is, you will get a different value for a depending on whether you solve at Δt = 1, Δt = 5, or Δt = dt. A change in the length of your vo vector will change the length of your a vector."
No, it won't: vo is a constant in the case you are offering. If you are just varying times to make vo change in length, you are talking about a particular given circle. You are not talking about any circle. Therefore, if you increase the Δt from one to five, for example, you are also increasing the distance along the vector: therefore the velocity stays the same. A shorter velocity vector in that case is not a different velocity; it is the same velocity measured over a shorter time. If you make the move from Δt = 5 down towards dt, and the triangle gets smaller, the value for vo does not get smaller. Velocity equals x/t, remember. The length of the vector expresses only the x, but the t is always implied.
We don't need to differentiate, because differentiation would yield a change in that vector. It would require us to consider the vector Δv a velocity, and we would be calculating a change in that velocity, a ΔΔv, during an infinitesimal interval dt. Not only is that unnecessary, it is absurd. If the vector were a velocity, it would not change over any interval, not a large interval or a tiny interval dt. Therefore a ≠ dv/dt nor dΔv/dt. Those equations would only yield a = 0. Δv is already a differential—it is the difference between two velocities—therefore it would be redundant to differentiate it. The Pythagorean theorem works at any t, even dt. But there is no limit here, since the value for a is the same whether you calculate it at any real interval (a large triangle) or near zero (a tiny triangle).
Think of it this way: the equation a = dv/dt describes a ratio of change between v and t. If v does not change as t changes, then v is a constant. The derivative of a constant is zero. Therefore it makes no sense to differentiate a constant velocity, even if it happens to be labeled Δv.
You may say, "OK, but is all that legal? Can you combine different vectors in a vector addition? Isn't there some rule about mixing acceleration vectors and velocity vectors?" Yes, there are rules. The length of the vector stands only for its numerical value: that's why you must keep careful track of angles. But no one has ever had any problem with the way that distance vectors and velocity vectors were combined in this problem, historically. The radius of the circle is obviously not a velocity; it is a distance. But both the textbook and Feynman use the radius and the velocity vectors as values that can be put in the same equation. If you can do that, why not use acceleration vectors as well? The answer is, you can, and Newton, the textbook and Feynman all do that, too. They just don't call attention to it. They solve this problem without ever defining their variables. The trick is, apparently, to fail to define anything: then everyone will accept it without question. But Feynman's vector Δv must also be an acceleration vector, just like mine. Why do you think it is labeled with a delta? A delta v is an acceleration. The vector makes no sense as a velocity, not in his diagram or mine. If Feynman had defined it as a velocity vector, then notice that that vector does not change in length all the way around the circle—if the motion is circular. If there is no change in that velocity vector, then a┴ must be zero. Neither the orbital velocity nor the tangential velocity (nor the vector Δv) change in magnitude over any interval, so calculating any change in any v, or an a that was a change in v, would only give us the number 0. The number we have always achieved in the equation a = v2/r for a can only signify the acceleration vector that I have just found.
Feynman says that a┴ = Δv┴/Δt. But Δv┴ is always the same in uniform circular motion, by definition. It is a constant in his diagram and mine. Therefore in his equation, a = 0. And we see yet another way that he finessed this proof. For that equation to work, v┴ would have to be a velocity vector. Otherwise the form of the equation makes no sense. In the vector diagram he labels the tangential velocity v1. Then he labels the perpendicular velocity Δv┴. One is a variable and one is a delta variable. For what reason? They are equivalent types of vectors according to this equation. If that is so, then Δv┴ should be labeled simply v┴. He does it to confuse the issue. He needs a number for Δv┴ to put into this equation: a┴ = Δv┴/Δt. And he does gets a number. That seems to imply that the equation will yield a non-zero number for a┴. But by his notation, what we really need to make the equation a real equation is this a┴ = ΔΔv┴/Δt. We need a change in his velocity variable—which he labeled Δv┴ for no reason. A change in his perpendicular velocity would then read ΔΔv┴. But ΔΔv┴ = 0.
If Feynman admitted that Δv┴ is an acceleration vector to start with, then I could answer that his equation does not work that way either. a┴ = Δv┴/Δt is false, since you would then have a┴ = a┴/Δt. The rest of his substitutions also get skewed if he defines Δv┴ as an acceleration vector. But it must be one or the other. It is either an acceleration vector or a velocity vector, but I have shown that neither works in his proof.
You may say that my Δv is a constant, too. Yes, it is a constant acceleration. But it is not zero, since I never differentiate it.
As a final proof that my analysis of a = Δv is correct, go back to the beginning of Feynman's proof. Remember that he said, "The acceleration tangent to the path is of course just the change in length of the vector." Aha! No differentiating or putting the change in length of the vector over Δt there. If you translate his quote into a mathematical equation, it reads, a║ = Δv. That is all. If the acceleration tangent to the path is figured in that way, why would the acceleration perpendicular be figured in some convoluted way? The answer: it is not. It is figured in exactly the same way.
Besides, with the tangent acceleration in his example, you can differentiate if you want: it doesn't matter as long as you use the correct velocity variable. If you differentiate v1 in his diagram (not Δv║), you get a║. You also get Δv║, since a║ = Δv║. In other words,
a║ = dv1/dt = Δv║ ≠ dΔv║/dt
likewise a┴ ≠ dΔv┴/dt
You cannot differentiate Δv┴ in order to calculate a┴, since Δv┴ does not change over time. And you cannot use Feynman's other tricks, since I have shown they are all dirty tricks.
Someone may notice that my equation gives the wrong notation for an acceleration. Yes, that is true. In using the Pythagorean theorem on the lengths of the vectors, I lost their full notation. I only found the length of the acceleration vector, which is to say its number value. However, I will show below that this is not crucial. I will also show that the notation in the current equation is incorrect.
As a final complaint, someone may notice that the vector Δv does not curve: how can it be an acceleration? A vector diagram is a conceptual simplification. The vector's length stands for the Δx and the direction stands for the direction, but nothing can show the change in time. It is understood that the same change in time underlies all the vectors. All the vectors in the diagram exist during the same time interval. But the t-variable is completely ignored. If you put an acceleration vector into a diagram, the same thing holds. The t-variable is ignored. But if you have an acceleration and the t-variable is ignored, then the vector does not curve. It looks just like a velocity vector. An acceleration curves on an x, t graph because you are plotting x against t. In these illustrations we are not plotting against t, we are ignoring t. Therefore, it is possible to have an acceleration vector in an illustration that does not curve. It is not possible to have a curve that is not an acceleration, but it is possible to have an acceleration that is not a curve.
Besides, we have accepted for centuries that the centripetal acceleration points to the center of the circle at every instant. Every time it is drawn in textbooks it is drawn as a straight line vector. If history has drawn it as a straight line vector, then I should not be taken to task for it.
The next thing to notice is that my new equation yields very similar proportions to the current equation between a, r, and vo. If you think that my equation looks completely different from the current equation, I encourage you to put some numbers into it. Yes, it yields different values in almost all situations, but those values change in almost precisely the same way as the current equation. Meaning that as r and vo change, the value for a increases or decreases at the same rate as the current equation. I encourage you to test out the equation before you dismiss it out of hand.
Now let's get back to my proof. My last equation is the relationship between acceleration and tangential velocity. What if we want orbital velocity?
As t→0, d→b and the triangle formed by vo, Δv, and b approaches becoming a right triangle, with the right angle at point B. You can see in my illustration that the angle at B is obtuse. But as the arc d gets shorter, the angle diminishes, reaching a limit at 90o. In that case,
b2 + Δv2 = vo2
As t→0, b becomes the orbital velocity vector vorb, which is what we seek.
vorb2 + Δv2 = vo2
From above, vo2 + r2 = (Δv + r)2
So, by substitution, vorb2 + Δv2 + r2 = Δv2 + 2Δvr + r2
2Δvr = vorb2
Δv = vorb2/2r
a = vorb2/2r
Δv = √ vo2 + r2) - r = vorb2/2r
vorb = √[2r√ vo2 + r2) - 2r2]
As some may be aware, I just solved the problem using Newton's own idea of an ultimate ratio. I have applied the Pythagorean theorem over the last interval of the series—an interval which is not zero. I treat it as a real interval, not as a mystical infinitesimal interval, nor as an "evanescent" (Newton's word) interval. It is a normal interval* and there is nothing to keep one from using the Pythagorean theorem over that interval.
I stress again that at the limit, the angle at B (between b and Δv) is 90o, but vo ≠ vorb. For vo to equal b, the angle at B would have to go past 90o. It would have to be slightly acute. But that implies a negative time interval. B therefore cannot go past 90o. 90o is the limit. And when the angle is at 90o, vo > vorb.
You can now see that this solution stands as a refutation of Newton's Lemma VII. Newton states that at the limit, the arc, the tangent and the chord are all equal. I have just shown that at the limit the arc and the chord approach equality, but the tangent remains greater than both. Newton applied his limit to the wrong angle. He applied it to the angle θ in my illustration above, taking that angle to zero. I have shown that the limit must apply first to the angle at B. That angle hits the limit at 90o before θ hits zero. Therefore, θ never goes to zero, and the tangent never equals the arc or the chord. This is why the acceleration never goes to zero (and neither does the versine, for those keeping score). If θ went to zero we could not calculate an acceleration.
Newton's states that BC is compounded of (is the vector addition of) Bc and cC, in the first illustration above. If this is true then the tangential velocity and the orbital velocity cannot be equivalent. That would make BC and Bc equivalent at the limit. That cannot be, since that would completely nullify cC at the limit. But cC is the acceleration vector. You cannot nullify that vector at the limit and then claim to derive it. The arc and the tangent cannot be equal. The orbital velocity and the tangential velocity are never equal.
If Lemma VII is false, Lemmae VI and VIII must also be false, since they both concern taking the angle θ to zero. I have shown that θ is not zero at the limit.
It helps me to think of it this way, when I am working in the ultimate interval: we cannot take quantities all the way to zero, since then our variables start to disappear. We do not take B all the way to A or let θ equal zero. We are in the last interval in the series; we are not at zero. Even the last interval must have dimensions, no matter how small they are. Some time must pass; some distance must be crossed. We seek the dimensions at the end of that first interval, not at the beginning of the first interval. The beginning of the first interval is zero. The end of the first interval is not. At the beginning of the first interval, sinθ = 0. At the end of the first interval, sinθ = Δv/vo ≠ 0. This is now generally understood, in some form or another. What is not understood, apparently, is that this dooms not only Lemmae VI, VII and VIII but all current derivations of circular motion and a = v2/r. The foundations of the calculus have been rebuilt since the time of Newton, but many of Newton's assumptions have remained standing within the old walls. They have never been thoroughly examined.
Circular motion is, at bottom, a rate of change problem. We have two changes happening at the same time. While the body is moving in a straight line it is also being accelerated toward a central point. But a rate of change problem implies change. Change happens only over definite intervals. If we take our variables to zero we cannot solve, since the changes have gone to zero and therefore the ratios have gone to zero. Forces also cannot act over zero time intervals. There is no such thing as an instantaneous force, by physical definition. A force must act over an interval. The definition of kinetic energy, as related to the force, makes this clear. A force must act through some time or distance interval in order to do work, which work is the transference and equality of the kinetic energy. The same thing applies to acceleration, although this is never made as clear in current definitions. A force must move a body through some time or distance interval in order to impart an acceleration. There is no force at a point or instant. Every force and every acceleration must act through some period of time. This is what Newton did not fully comprehend and what current physics and calculus cannot comprehend.
*For further clarification, see my paper A Redefinition of the Derivative—why the calculus works and why it doesn't (2003).
I have solved this problem using Newton's idea of the ultimate ratio, since it mirrors the current conception of the calculus in most ways. I have corrected Lemma VII, but this has not affected my ability to use the historical concept of the limit. In my opinion, this concept of the limit is still overly complicated. There is an even easier method to the solution of any curve, without using limits or "infinite" series. However, use of that method requires knowledge of my paper on the foundation of the calculus, knowledge of which I could not take for granted in this paper. I believe that my arguments here are clear enough in the present form, making it unnecessary to include that method in this paper.
Part Six
Implications
We have seen that no matter which velocity you assign v to in the final equation—either orbital or tangential—
a ≠ v2/r.
You may ask, "Well, which is it? Which of your new equations are you proposing as a replacement for a = v2/r?" Notice that one factor in this decision might be supplied by Newton himself, for in the proof I mentioned in the beginning for deriving Kepler's third law from his gravity equation, he uses this step:
v = 2πr/t
where t is the period of the orbit, and 2πr is the circumference of the orbit. It is clear that this v is the orbital velocity here. For his derivation to work, v in equation a = v2/r must be the orbital velocity. And according to his math, my correction would not affect his derivation of Kepler's law. It only changes the constant:
t2/r3 = 2π2/GM instead of 4π2/GM
However, that leads us into the final embarrassment in this whole ignominious history of blunders. Not only is it now clear that Δv is not a velocity, vorb is also not a velocity. Newton's orbital velocity is not a velocity. This should come as no shock, since a velocity cannot curve. Every calculus curve tells us this. The whole history of circular motion tells us this. A curve is an acceleration. The orbital "velocity" is a complex motion made up of the tangential velocity and the centripetal acceleration. Feynman and the textbook should have already known this, since it is one of the conclusions of the whole problem, but for some reason they kept calling it a velocity and treating it as a velocity in the derivation of a. They differentiated it as a velocity; put it into acceleration equations as a velocity; notated it as a velocity. They acted for some reason as if the orbital velocity was known, and we were deriving the acceleration from it. They acted this way because they had a number for it from the equation above, v = 2πr/t. It was easy for them to calculate: orbital "velocities" are the easiest thing in the sky to calculate from visual data. Therefore they thought they understood it. But they didn't, as is clear from these failed derivations.
Newton didn't understand it either, for he substitutes v2/r for a as if v is a velocity. In the Kepler proof he lets
ma = mv2/r.
That looks very familiar, in a dangerous way, if you don't know that the v is really an acceleration. That could lead us into kinetic energy problem meltdowns that equal this one. There is no reason why we should still be labeling the orbital velocity as a velocity.
A reader may well ask how this finding can be commensurable with current engineering and applied physics. We have loads of empirical evidence that the historical equation is true. Newton was trying to derive an equation that he already knew was true from data he had on hand. Therefore the historical equation a = v2/r is deriving for us a relationship between the centripetal acceleration and 2πr/t. We have need of this relationship and can make use of this relationship in physical calculations, despite the fact that the second value is not a velocity. For the sake of convenience, we have labeled it a velocity and gone on with our business. These two equations work together, because they are correct relative to eachother. That is to say, if a = v2/r, then v = 2πr/t. But the fact is, neither one is true. The orbital acceleration is really aorb = 2√2πr/t, and the relationship is a┴ = aorb2/2r.
What this means is that our current equations are just straightforward heuristics. We use them all simply due to the fact that it is easy for us to measure 2πr/t. That is our basic data, data that we like and always have liked, and whether 2πr/t is a velocity, an acceleration, or none of the above, has never really mattered to us. Newton was trying to develop an equation that contained this data, and he did that. He developed a true equation that relates a and 2πr/t. Unfortunately, he labeled 2πr/t as the orbital velocity, and it is not the orbital velocity. Nor is it the orbital acceleration. It is just a relation of two variables and a constant. Because Newton derived a true equation, it has not mattered much (in most situations) that his variable assignments were sloppy. As long as we remember that the v variable in the equation a = v2/r is equal to 2πr/t, we cannot go wrong. But we have not always remembered this, as I will show with Bohr and quantum mechanics.
I have shown that the circle describes not a velocity, but an orbital acceleration. This acceleration is the vector addition of the tangential velocity and the centripetal acceleration. To find it we use the equation a┴ = aorb2/2r. Using this equation, we find that
(2πr/t)2/r = aorb2/2r
aorb = 2(√2)πr/t
a + r = √(vo2 + r2)
a2 + 2ar = vo2
vo = a√[1 + (2r/a)]
This is another very useful new equation for tangential velocity. It will allow us to calculate velocities and energies that have so far eluded us, such as the energy of a photon emitted by an electron in orbit.
The answer to the question, "which of my equations must replace the current one?" is therefore the first one:
a = √ vo2 + r2 ) - r. If we want an equation that relates the velocity of an orbiting object to its centripetal acceleration, we must use this equation, since it is the only equation with a true velocity variable in it. This works out in other ways, too, since the proportions of the variables in that equation remain the same as the historical equation, while they don't in the equation a = vorb2/2r
Which brings up another problem. You can see that physics has never had a way to measure tangential velocity. "Orbital velocity" can easily be measured by circumference per time of one revolution. But tangential velocity must be calculated. You can calculate using my new equations, but before this paper there was no equation from orbital to tangential velocity. Neither Feynman nor any of the textbooks were even clear on the difference. I assume this means that no one was clear on the difference. [Notice that Newton also could not calculate from one to the other, since according to lemma VII they were the same thing.]
Both theoretical scientists and engineers should understand that such mistakes as this one ultimately lead to ruin. In the short term they may lead to simple engineering failures, which is bad enough. But in the long term they always lead to theoretical dead-ends, since a sloppy equation is the surest of all possible ways to stop scientific progress. A correct equation is almost infinitely expandable, since its impedance is zero. Future scientists can develop it in all possible directions. But a false or imprecise equation can halt this development indefinitely, as we have ample proof. Mislabelling variables is not a semantic or metaphysical failure. Is it failure of science itself.
All this is very big news, I hope you will agree. What makes it even bigger is that I will show in subsequent papers that this is far from the only basic equation that is fatally flawed. In putting physics under a microscope, I have found that the sloppy algebra and calculus exposed above is the rule, not the exception: one might say it is pandemic. It infects the entire field, including the highest levels. Modern scientists and mathematicians have proven themselves more interested in juggling complex matrices and other higher math than in mastering high-school algebra. Which is precisely why such an error in derivation was left standing for so long.
Much work is left to be done in basic physics, despite the hubristic claims of many that the field is nearly complete. In my opinion, the most important and immediate work to be done is in conceptual analysis—in combing the mass of theoretical and mathematical work already done, and making it consistent. This will be achieved not with so-called higher math, in which the original concepts get lost; nor with the esoteric theories of the scientific avant-garde, in which the production of paradoxes becomes a sign of distinction; but with simple algebra, in which the concepts are kept near the surface at all times.
I have led my attack with this short and shocking paper because I know that only a full-frontal assault has any hope of breaching the walls of science. Philosophical subtleties can always be dismissed as arbitrary or subjective or metaphysical, but I hope it is impossible to ignore simple math.
I have now found other mathematical proof that the current equation is wrong, since I have shown in my paper on the virial that the 2 in the equation 2K = -V is an outcome of this bad equation. We are told that the potential energy in the virial is twice the kinetic energy, but that has always been illogical. By correcting the equation a = v2/r, I am able to correct the equation 2K = -V, making it K = -V. This not only makes the virial logical, it acts to confirm my correction in this paper. The two corrected equations confirm one another.
For more on this problem, go to my newer paper on pi, and my newest paper on a=v2/r.
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.