return to homepage ON LAPLACE
return to updates
AND THE
3-BODY PROBLEM
by Miles Mathis
First posted August 26, 2009
In a recent paper on atheism I claimed that Laplace had not perfected the equations of motion of Newton, and that his real legacy was in “mucking them up” with more math so that the holes in celestial mechanics were even harder to see. Some readers did not like this, despite my link to my own paper on celestial mechanics, where I spend several paragraphs talking about Laplace. Their problem was that although I had mentioned Laplace, and although I had indeed shown big holes in current theory, I had not shown how Laplace had failed to do what he is claimed to have done, or how he is guilty of a cover-up. Fair enough. My celestial mechanics paper is thin on Laplace, and a reader must extrapolate pretty far to see how Laplace is at fault. So I will do the extrapolation for you here.
Among other things, Laplace is famous for extending Newton's equations of motion into specific problems in the solar system, specifically the perturbations between Jupiter and Saturn. It had been known for some time that the orbit of Saturn was getting a bit larger and that of Jupiter a bit smaller. What was required was for mathematicians to match the equations to the data. Euler and Lagrange had made some headway on the problem, but it was far from solved when Laplace tackled it 1776. His first assays were not fruitful, the very first being an attempt to consider the action of an ether. Remember that, because I will show that he was right, as a matter of mechanics, the first time. There is no ether, but the perturbations are not simply gravitational, either. The perturbations are also electromagnetic.* They are caused by the unified field, and therefore cannot be explained by straight pulling forces alone. At any rate, he soon gave up on mechanics and returned to a strictly heuristic and mathematical solution. That is, he did not consider the causes of the forces, he considered only their sizes. He wanted to match the math straight to the data, in the modern way. That is why modern physicists love him.
[*see my new papers on Axial Tilt and Bode's Law for the equations that prove this.]
Euler had at first considered only the mean elongation, or the straight-line distance between the planets and sun. If gravity as a straight pulling force were the only mechanism in celestial mechanics, this should have gotten the right answer, which is precisely why these great mathematicians were stumped for so long, and why Laplace was looking at an ether 30 years after Euler's failure. Newton's equations don't use or support an ether, but the equations and theory of Newton weren't matching the data, so Laplace was a bit desperate. Euler next tried factoring in the eccentricities, but using Newton's theory, these should not make any difference. The shape of the orbit should not matter in Newton's equations, since it is the distance between the objects that determines all the forces. And, indeed, the eccentricities did nothing to help solve the problem. So Lagrange and Laplace began to look at secular equations, or, in other words, at the magnitude of the remaining inequalities. Again, these should not make any difference if Newton's theory is correct. In fact, using Newton's equations should not provide us with any inequalities, since inequalities are defined as irregularities in the orbit beyond the straight gravitational pulls. But Newton does not allow for this. The only way to mechanically account for these inequalities, using straight pulling forces, is to assign them to still more bodies, like Uranus or Neptune, but this is not what Laplace did. Why? Because Neptune was not discovered yet, and Uranus was only just discovered (1781) and they didn't have any good data on it.
Besides, the “great inequality” between Jupiter and Saturn is still not thought to be caused by Uranus or Neptune or any other gravitational perturbations. It is now said to be caused almost entirely by the 5:2 resonance of the two orbits.1 But as I have already shown in my gravity papers, these resonances cannot be caused by gravity alone. The modern argument is circular: a resonance is just a number relation, a mathematical outcome, and cannot be a cause of anything. The modern argument claims that the resonance is caused by gravity and that the great inequality is caused by gravity, and then that the great inequality is caused by the resonance. That is not a logical line of cause. That is like saying that Jan gave birth to Bob and Jan gave birth to Jim, and that Jim is the cause of Bob.
The great inequalities are actually not anything mechanical or mathematical. The “inequality” is just a name that Laplace made up to give to the gap he needed to fill between what Newton's math could really explain, using the mean elongations, and what the visual data was telling him. It was not an inequality, it was a margin of error. And he filled it just as I claimed in the other paper, by finessing the math. Laplace was a master of this, just like all the other big names would be from then on, from Gauss to Hilbert to Feynman to Witten. A good mathematician should always be able to push a set of equations a few percentage points, and that is all he needed.
Laplace's solution is a clear fudge, because the forces between the objects, if caused by Newton's gravity, can only be a function of the distances between them. The eccentricities, inclinations, and mean motions cannot have anything to do with it, much less the third and fourth powers of these numbers. Laplace, like so many others, uses the calculus only as a trick to allow him these higher terms, by expanding things that aren't really expandable. What I mean is, Laplace doesn't need to look at the equations for the orbits themselves. He doesn't need to concern himself with curves, neither circles nor ellipses. He only needs to know the distances between his three objects, which are straight-line distances. Then he can integrate these over time. This is why Euler's first solution should have gotten the right answer. But by looking at curves, Laplace is able to expand the equations into infinite series, using tricks based on Newton's own binomial expansion (think power series). Any curve equation can be expanded into an infinite series like this, because a curve is based on powers above 1. The curve is a series of differentials and a differential is a binomial.
This trick is still being used today, as I have shown recently with gamma. Because Einstein's gamma contains a square root, it can be expanded into an infinite series. This infinite series can then be used to show higher orders of numbers, and these orders can be interpreted in various sloppy ways. But since I have shown that gamma is derived incorrectly, and have shown that the real transforms do not contain a square root, all the interpretations, now called parameterized post-Newtonian formalisms, are false.
It is the same with Laplace. Laplace interprets these higher orders as inequalities, but they are not inequalities, they are terms in the expansion. You cannot treat terms in the series separately, as if they have some life of their own. Specifically, you cannot assign them to unknown perturbations or to your margins of error. Einstein makes a similar mistake when he assigns the first term in his expansion (which is 1) to Newton's field, and the other terms to relativistic corrections. He can't do that, because in a series expansion the terms may not be read that way. The series is not just as list of terms separated by commas, it is a list of terms that must be added. Notice the plus signs in the expansion!
This is of paramount and fundamental importance, because although Laplace may be able to match data by manipulating these terms over longer periods, in doing so he is obscuring the mechanical cause of the perturbations. Not only is he not able to show the mechanics underneath his math, his math acts as a heavy blanket, keeping future physicists and mathematicians from questioning what his math tells us about the field it is representing. And it tells us some very strange things indeed!
Before I show those strange things, let me clarify the previous paragraphs. Laplace's first trick is to completely ditch Newton's own equations and theory. Laplace doesn't use Newton's equations, or Kepler's either. Why should he, since they are known to fail? No, he makes up his own equations, based upon the observations themselves. In Forest Ray Moulton's book from 1914, which is published in full on the web by Google Books2, you can see (p.202) that Laplace uses the first and second derivatives of the direction cosines, and these angles are taken directly from the three or four real observations.
d2x/dτ2 = -x/τ3
d2y/dτ2 = -y/τ3
d2z/dτ2 = -z/τ3
x = ρλ – X
y = ρμ – Y
z = ρν – Z
[I refer to Moulton's book because, besides being completely orthodox on this question, it is easy to find, whereas the English translation of Laplace by Bowditch is out of print, unavailable on the internet, and otherwise difficult to find.] In other words, the angles aren't based on calculations from Newton's equations or theory, they are taken directly from the data. If this data doesn't fit Newton's theory (and it doesn't), then Laplace will have directly bypassed the theory at this point. From the very first step, Laplace has detached his math from Newton, attaching it instead to the data.
You will say, fine, good for him. As scientists we are interested in the data, first and foremost. Yes, Dr. Feynman, but if you have bypassed the theory on your first step, you cannot later claim to have confirmed the theory, can you? If the real observations were in strict agreement with Newton, Newton would not have had to propose a hand of God, Halley would not have shown a problem in the orbits, and Euler would have had no trouble finding a solution. Laplace was working on the problem precisely because the data did not match the prediction of gravity as a simple straight-line pull in the three-body problem. Laplace's solution is a solution of the data, not of Newton's theory. Laplace finds a way to solve the equations, by discovering the finer resonances they contain, but because his initial equations were taken from the data, he cannot, at the end, claim to have discovered a solution that completely confirms Newton or that proves the stability of the solar system. In fact, he has done precisely the opposite. He has proved that the three-body problem can be solved only by going well beyond Newton's math and postulates and theory.
My critic will say, "What do you mean he attached the equations to the data? Didn't he just create equations to contain the data, like anyone else would?" No, look at his equations. All you have is accelerations and directional cosines. You don't have any representation of the fields present, and Newton's theory is a field theory just as much as Einstein's. Newton's gravity is a mass field, since his masses determine all forces and the forces determine the accelerations. Just imagine that you wanted to fit in my charge field here, so that the final accelerations were caused by not one but two separate fields acting in tandem. You couldn't do it, because Laplace has already begun differentiating from the first step. The acceleration is a single differential in each dimension, so that it can be differentiated or integrated in only one manner. The second derivative of x, for instance, cannot be manipulated in two different ways at the same time. But if each acceleration is caused by two forces, and these forces vary in different ways, then Laplace will have closed out any possibility of correct mathematical representation of his force fields. Even in the case that he brings mass back into the equations later, he still will not be able to represent all the variations in the fields. This may be why he gave up on the idea of the ether early on. You see, he doesn't need an external ether, acting independently of his mass field. He needs his "ether" to already be inside his equations from the first step, because Newton's ether in already inside his equations (unknowingly). As I have shown, Newton's main gravity equation works in most situations because it already contains the E/M field (and the E/M field is a sort of ether, roughly). This is why he needs G in the equation: it acts as the scaling transform between his two fields. But Laplace can represent none of this, since his equations are not proper field equations. He doesn't have enough complexity in his initial representations of the orbits to show all the field variations. In modern terms, he doesn't have enough degrees of freedom. The real field in the solar system has two acceleration fields, not one, even before you get to relativity, and Laplace has no way to represent that. His equations aren't even as good as Newton's, since Newton has not one but two masses in his main equation. Because he starts with these masses, not written as derivatives or partial derivatives, we can split each mass into volume and density variables. This immediately gives him twice as many degrees of freedom as Laplace has here. We can give volume to one field and density to the other, so that (in most cases) both will be represented in the final solution. This is precisely why Newton's equation works in real life, despite the fact that no one has ever been able to unwind it.
I will now show the oddest thing in the entire history of this problem. It is fantastically odd, not only in itself, but because no one in history, not even Laplace or Lagrange or Euler, ever made comment on it, to my knowledge. If they ever saw this fact underneath their numbers, they must have swept it under the rug. Or perhaps the fact has been excised from history, by one group or another. My mother (who has a PhD in mathematics, and who scored 800 on her math GRE in 1960, when the 99th percentile for women was 650) taught me to approach all math problems by first estimating a ballpark solution. Whenever possible, I should look at the problem intuitively or spatially or in a commonsense fashion, and this would keep me from moving toward answers that were clearly illogical. In other words, look at the mathematical problem without math, to start with. Let us do that with this problem of Jupiter and Saturn. Let us strip it of all math and all complications, and see what we would expect, using the pretty simple postulates of Newton. Let us look at four positions of the two planets, in four diagrams, in a straight 3-body problem.
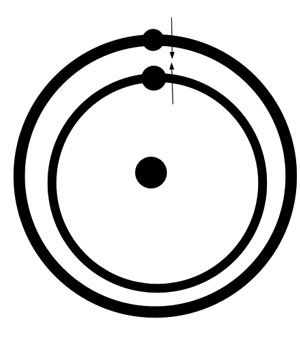
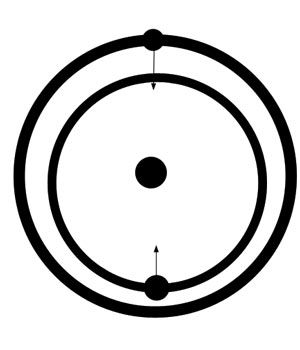
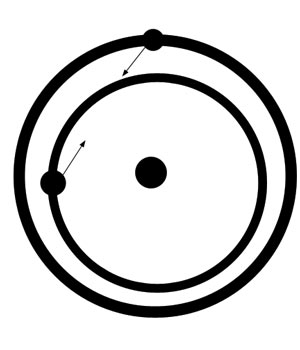
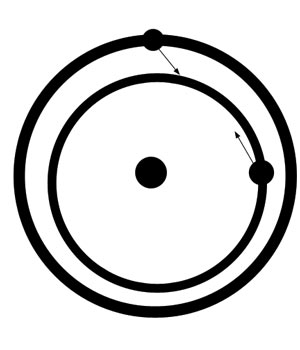
With gravity as a force of attraction, and no other force fields playing a part, we find that we would expect the gap between Jupiter and Saturn to be getting smaller. Because, while Jupiter is sometimes being pulled away from the Sun by Saturn and sometimes toward it, Saturn is always being pulled toward the Sun by Jupiter. I challenge you to find a relative position of the two planets where Saturn is not being pulled into a lower orbit by Jupiter.
In fact, Saturn could not be pulled into a higher orbit, even over a single differential, unless Jupiter went above it. In other words, the orbit of Jupiter would have to be so highly eccentric that Jupiter's semi-major axis would have to exceed that of Saturn's for some part of their combined orbits. And even then, Saturn's orbit would be increasing over only a small span of years. It could not increase, as a whole, from the time of Chaldea or Ptolemy until the time of Laplace. It is clear from the simplest analysis that Saturn cannot go higher due to the laws of Newton, without the influence of outer planets. But Uranus and Neptune were not included in Laplace's perturbation math. It is strictly impossible for Laplace to have proved what he is said to have proved.
For this simple reason, you can dismiss any and all claims to the contrary, no matter how much impressive math or argument they throw at you. You cannot prove something that is impossible, and if someone does prove it, you can be sure they cheated. You can spend a lot of time finding the specific cheats, or you can just use the simple proof. They cannot have proved it, because you have already proved that it is impossible.
My critic will claim that it is quite easy to imagine the gap between Saturn and Jupiter getting larger or the orbit of Saturn increasing, even given my figures. Since the orbit of Saturn is slightly elliptical, we just need to go to Saturn's nearest approach to the Sun. The differentials after that will all show a larger orbital distance, no matter what Jupiter is doing. Yes, but that is not what Halley found, is it? Halley was not talking about a short-term increase in the orbit of Saturn, during one of its 30 year cycles. Halley was talking about an increase over centuries. My simple diagrams show that the only long-term change in Saturn's orbit we could expect, as a function of a pulling perturbation from Jupiter, is a going lower. The only perturbation from Jupiter that would send Saturn higher over the long term is repulsion. That is so clear from the first look that I can't believe I am on this page having to say it. In no part of any long-term cycle could the orbit of Saturn, as a whole, appear to increase, given gravity alone.
All Laplace did is assume long-term stability of the solar system, and then find a math to match the given data. But this is a double cheat, 1) because gravity by itself cannot explain the given curves and motions, and 2) because this assumption of long-term stability is clearly false. Just as Laplace could not have proved that Newton's equations explain the perturbations of Jupiter and Saturn, he could not have proved stability, since there is no stability. To this day, this question of stability commands much time and effort and verbiage3, but all you have to do is look at the asteroid belt to answer it. If the solar system is stable, why do we have so many obvious indications of collision, and this magnificently obvious proof of major collision?
The standard model in this area now claims that the asteroid belt was never anything but collection of debris left over from the solar disk or nebula. Their main argument in this regard is that the debris we have studied varies in chemical composition, so it could not have come from a single planet. The combined mass of the debris is also low, so it would have to be a very small planet. But neither of these arguments is strong at all. If we pulverized the Earth or Moon down into tiny fragments, we would also find chemical variation, since the core differs greatly from the crust. The asteroid belt is likely the remains of at least two planets, since we propose a collision, not a natural breakup. Planets vary greatly in chemical composition. As for the low combined mass, that is also easy to answer, since a large part of the mass must have been ejected immediately from the area in collision. More would have been lost over time to collision and ejection, so that even if the collision were fairly recent, we would expect only a fraction of the original masses to remain in the area. But the best argument for a breakup of a planet already at that orbit is the low amount of collision we see today. The residual pieces are amazingly stable at that orbit and trajectory, and that is probably because they were already at that orbit and trajectory to start with. This is the residue that avoided great momentum changes during the first impact. Planetoids and debris herded into this area by Jupiter would be prone to collision, unless they were all herded from the same area at the same time. And debris left over from the nebula would have to be incredibly stable to have come down to us in this fashion, staying in a primordial state while all around them evolved into open space or major planetary orbits or satellites. Finally, the model now states that the planetesimals in the asteroid belt were too perturbed by Jupiter to form a planet; but Jupiter's own moons, perturbed both by Jupiter and by Saturn, are not too perturbed to be large and round and orderly (large and round compared to the planetesimals, anyway). Rather than herding the planetesimals and preventing them from combining, it is much more likely that Jupiter has stolen many of them, making them into its smaller satellites. No, modern theory on the asteroid belt is just another example of the de-evolution of science and rationality. Until the last fifty years, the shattered planet hypothesis was widespread, since it is so obvious, and only now, when we cannot stand the idea of instability, are we forced to retreat into counterintuitive models.
[See my new paper The Main Cause of Solar System Instability for more on this.]
The great mystery of the asteroid belt is Ceres, which is nearly perfectly round and amazingly pristine. It is like nothing else in the belt. Most likely it was the distant moon of the planet hit, and thereby avoided the brunt of the first collision. To explain its non-ejection from the main orbit upon the loss of its primary, we only need to imagine it was moving parallel to the primary at impact, in one of two orbital positions. And its composition may give it a high electromagnetism, which would repel other slow-moving intruders in the belt. It is already proposed to have a high water content (as ice) and water is a very good conductor, as is known.
But back to Laplace. Can we propose a solution? Well, we know from observation that Saturn is in fact going higher, at least over part of its long-term journey. And we know that gravity by itself cannot account for this. Which means that something else must be causing the resonance and the long-term motion. We must have gravity PLUS something else. This is why Laplace first looked at the ether. He must have known what I have just proved, and he wanted to solve it without leaving Newton completely in the bin. An ether would have been calculable as a straight addition to Newton, and Laplace could then hope to match the pair to the data, truly saving Newton. Besides my many papers on the foundational E/M field, which clearly show the E/M field already existing within the equation of Newton, physics has long had ample data that the planets have strong E/M fields, easily strong enough to be included in perturbation theory. Magnetospheres, solar wind exclusion (with and without a magnetosphere), plasma research, tangential torques on planets and satellites by their primaries (unexplainable by gravity, which cannot work at a tangent), and so on. In the 50's it was discovered that Jupiter was sending out strong radio noises (predicted, amazingly enough, by Velikovsky), and more recently similar noises were found coming from Saturn. You can hear this “Saturn singing” by going to ABC, which has a copy of NASA's own tape.4 Beyond that, it has long been known that the Moon strongly affects radio reception, causing a complete doubling. Also in the 50's, John H. Nelson of RCA showed that the planets strongly affect radio transmission as well, and that a clear “electrical balance mechanism” was at work among all the bodies of the solar system. All these signals, noises, and effects are direct evidence of electrical perturbations. If the mainstream have ignored them or buried them, that is not proof they do not exist.
It is claimed that these electrical effects aren't strong enough to enter Laplace's or Newton's equations, but I have shown that they are. Using simple calculations and postulates, I have shown that the charge perturbation from the Moon to the Earth is about .151 m/s2, or about .46% of the total or unified force between them. That is far from negligible. Moreover, the charge perturbation is positive or repulsive. Yes, the foundational E/M perturbation is always opposite to the gravitational force, and this must affect all the terms in any equations of motion.
My critic will say, “Even if you are right in all this, we still can't send Saturn higher unless the E/M component of the unified field is shown to be larger than the gravity component. To send Saturn higher requires a straight repulsion, and as long as the gravity component is larger than the E/M component, the unified field must remain attractive, as a total force. You have shown that the E/M component is much smaller than the gravity component. So your theory does not help us. The unified field must still always be attractive.” That is logical as far as it goes, but it doesn't take into account the nature of the E/M field. Yes, when we look at highly stable and nearly round orbits like that of the Moon, the E/M field is not doing a lot of the work. The Moon is moving quite fast at a good distance, and the effective E/M repulsion between the Earth and Moon can be quite low. But I have shown that the E/M field is capable of very quick response and enlargement, since it varies to the fourth power, not the square. In other words, if we bump the Moon into a lower orbit all of the sudden, say half of its distance now, the E/M field repulsion between the two bodies will immediately increase by a factor of 16. This difference in field variation between the E/M field and gravity is precisely what gives the orbit its “float.” As I showed in my celestial mechanics paper, real orbits have much more stability than can be accounted for in Newton's or Einstein's theories. Even Kepler's theory of ellipses cannot work without a large degree of float or correction. Neither circular orbits nor ellipses can be explained with pulling forces alone, since a balance of two motions or forces (gravity and tangential velocity) cannot be stable. It requires three motions to create stability over a series of intervals. Because the push (E/M) varies more quickly than the pull (gravity), we have three motions that can correct themselves against eachother, creating long-term stability.
This solves the problem of Saturn, because we can now explain the resonance in a logical and mechanical fashion, without using fancy math to hide it or big names to shoo off analysis. It was known even in the time of Halley that this divergence in the orbits of Saturn and Jupiter meant that they must have been quite near eachother millions of years ago. If we reverse time, the two orbits must get nearer and nearer. Laplace showed that they wouldn't have collided, because the resonance causes the orbits to begin separating again, after a long space of years. He showed that what we have is a dance, where they are moving away for half of the long period and moving closer for the other half. All good, except that using his math, and the theory of gravity, you can't explain why this is. As Jupiter and Saturn get nearer, they should attract eachother more, not less, right? It is the mechanics that causes the math, not the math that causes the mechanics. The math is a representation of physical causes, the math is not the cause itself. So we must have some reason that Jupiter and Saturn decide to start moving away from eachother again, despite being brought together. Newton, Kepler, Laplace, and Einstein can't explain it, which is why it has been buried up to this day. No one wants to admit that the problem exists, so they pile century after century of math on top of it, to hide it. Even Laplace's equations weren't thought to be sufficient, so Poincaré is used to create a deeper pit.
But the solution is quite simple, once you know that the E/M field is available, and that it changes to the fourth power. When you bring Jupiter and Saturn near to eachother, the E/M repulsion kicks in very strongly, and the closer they get, the stronger it gets. It bounces them apart, in the same way the Sun bounces a comet away. Gravity cannot create such a “well” on its own. So-called gravitational wells are real, but they can only be caused by the unified field, or the E/M field and gravity working in tandem, as I show in my paper on the ellipse. This explains the point of greatest divergence of the orbits of Jupiter and Saturn as well, because as the orbital gap increases, the repulsion of the E/M field shrinks rapidly. A quick shrinking of the E/M field strength is the same as a quick building of the unified field strength, and Jupiter is able to pull Saturn back in line, assuring that Saturn's orbit does not continue to grow indefinitely.
Postscript: I have now calculated the distance of closest approach of Jupiter and Saturn in this resonance.
To see some specific examples of the charge field in historical perturbation equations, you may read my newer paper on this, which extends my comments on Newton, Laplace, Clairaut, and others.
2http://books.google.com/books?id=0ZwRAAAAYAAJ&pg=PA429&dq=laplace+celestial+mechanics&lr=#v=onepage&q=laplace%20celestial%20mechanics&f=false
3http://www.scholarpedia.org/article/Stability_of_the_solar_system
4http://www.abc.net.au/science/news/stories/s1425596.htm
If this paper was useful to you in any way, please consider donating a dollar (or more) to the SAVE THE ARTISTS FOUNDATION. This will allow me to continue writing these "unpublishable" things. Don't be confused by paying Melisa Smith--that is just one of my many noms de plume. If you are a Paypal user, there is no fee; so it might be worth your while to become one. Otherwise they will rob us 33 cents for each transaction.